The First Law of Complexodynamics
A few weeks ago, I had the pleasure of attending FQXi’s Setting Time Aright conference, part of which took place on a cruise from Bergen, Norway to Copenhagen, Denmark. (Why aren’t theoretical computer science conferences ever held on cruises? If nothing else, it certainly cuts down on attendees sneaking away from the conference venue.) This conference brought together physicists, cosmologists, philosophers, biologists, psychologists, and (for some strange reason) one quantum complexity blogger to pontificate about the existence, directionality, and nature of time. If you want to know more about the conference, check out Sean Carroll’s Cosmic Variance posts here and here.
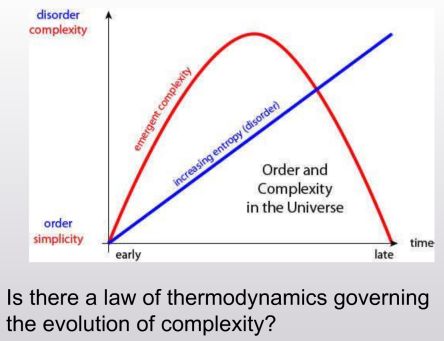
Sean also delivered the opening talk of the conference, during which (among other things) he asked a beautiful question: why does “complexity” or “interestingness” of physical systems seem to increase with time and then hit a maximum and decrease, in contrast to the entropy, which of course increases monotonically?
My purpose, in this post, is to sketch a possible answer to Sean’s question, drawing on concepts from Kolmogorov complexity. If this answer has been suggested before, I’m sure someone will let me know in the comments section.
First, some background: we all know the Second Law, which says that the entropy of any closed system tends to increase with time until it reaches a maximum value. Here “entropy” is slippery to define—we’ll come back to that later—but somehow measures how “random” or “generic” or “disordered” a system is. As Sean points out in his wonderful book From Eternity to Here, the Second Law is almost a tautology: how could a system not tend to evolve to more “generic” configurations? if it didn’t, those configurations wouldn’t be generic! So the real question is not why the entropy is increasing, but why it was ever low to begin with. In other words, why did the universe’s initial state at the big bang contain so much order for the universe’s subsequent evolution to destroy? I won’t address that celebrated mystery in this post, but will simply take the low entropy of the initial state as given.
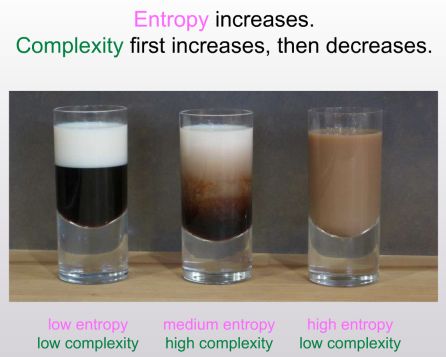
The point that interests us is this: even though isolated physical systems get monotonically more entropic, they don’t get monotonically more “complicated” or “interesting.” Sean didn’t define what he meant by “complicated” or “interesting” here—indeed, defining those concepts was part of his challenge—but he illustrated what he had in mind with the example of a coffee cup. Shamelessly ripping off his slides:
Entropy increases monotonically from left to right, but intuitively, the “complexity” seems highest in the middle picture: the one with all the tendrils of milk. And same is true for the whole universe: shortly after the big bang, the universe was basically just a low-entropy soup of high-energy particles. A googol years from now, after the last black holes have sputtered away in bursts of Hawking radiation, the universe will basically be just a high-entropy soup of low-energy particles. But today, in between, the universe contains interesting structures such as galaxies and brains and hot-dog-shaped novelty vehicles. We see the pattern:
In answering Sean’s provocative question (whether there’s some “law of complexodynamics” that would explain his graph), it seems to me that the challenge is twofold:
- Come up with a plausible formal definition of “complexity.”
- Prove that the “complexity,” so defined, is large at intermediate times in natural model systems, despite being close to zero at the initial time and close to zero at late times.
To clarify: it’s not hard to explain, at least at a handwaving level, why the complexity should be close to zero at the initial time. It’s because we assumed the entropy is close to zero, and entropy plausibly gives an upper bound on complexity. Nor is it hard to explain why the complexity should be close to zero at late times: it’s because the system reaches equilibrium (i.e., something resembling the uniform distribution over all possible states), which we’re essentially defining to be simple. At intermediate times, neither of those constraints is operative, and therefore the complexity could become large. But does it become large? How large? How could we predict? And what kind of “complexity” are we talking about, anyway?
After thinking on and off about these questions, I now conjecture that they can be answered using a notion called sophistication from the theory of Kolmogorov complexity. Recall that the Kolmogorov complexity of a string x is the length of the shortest computer program that outputs x (in some Turing-universal programming language—the exact choice can be shown not to matter much). Sophistication is a more … well, sophisticated concept, but we’ll get to that later.
As a first step, let’s use Kolmogorov complexity to define entropy. Already it’s not quite obvious how to do that. If you start, say, a cellular automaton, or a system of billiard balls, in some simple initial configuration, and then let it evolve for a while according to dynamical laws, visually it will look like the entropy is going up. But if the system happens to be deterministic, then mathematically, its state can always be specified by giving (1) the initial state, and (2) the number of steps t it’s been run for. The former takes a constant number of bits to specify (independent of t), while the latter takes log(t) bits. It follows that, if we use Kolmogorov complexity as our stand-in for entropy, then the entropy can increase at most logarithmically with t—much slower than the linear or polynomial increase that we’d intuitively expect.
There are at least two ways to solve this problem. The first is to consider probabilistic systems, rather than deterministic ones. In the probabilistic case, the Kolmogorov complexity really does increase at a polynomial rate, as you’d expect. The second solution is to replace the Kolmogorov complexity by the resource-bounded Kolmogorov complexity: the length of the shortest computer program that outputs the state in a short amount of time (or the size of the smallest, say, depth-3 circuit that outputs the state—for present purposes, it doesn’t even matter much what kind of resource bound we impose, as long as the bound is severe enough). Even though there’s a computer program only log(t) bits long to compute the state of the system after t time steps, that program will typically use an amount of time that grows with t (or even faster), so if we rule out sufficiently complex programs, we can again get our program size to increase with t at a polynomial rate.
OK, that was entropy. What about the thing Sean was calling “complexity”—which, to avoid confusion with other kinds of complexity, from now on I’m going to call “complextropy”? For this, we’re going to need a cluster of related ideas that go under names like sophistication, Kolmogorov structure functions, and algorithmic statistics. The backstory is that, in the 1970s (after introducing Kolmogorov complexity), Kolmogorov made an observation that was closely related to Sean’s observation above. A uniformly random string, he said, has close-to-maximal Kolmogorov complexity, but it’s also one of the least “complex” or “interesting” strings imaginable. After all, we can describe essentially everything you’d ever want to know about the string by saying “it’s random”! But is there a way to formalize that intuition? Indeed there is.
First, given a set S of n-bit strings, let K(S) be the number of bits in the shortest computer program that outputs the elements of S and then halts. Also, given such a set S and an element x of S, let K(x|S) be the length of the shortest program that outputs x, given an oracle for testing membership in S. Then we can let the sophistication of x, or Soph(x), be the smallest possible value of K(S), over all sets S such that
- x∈S and
- K(x|S) ≥ log2(|S|) – c, for some constant c. (In other words, one can distill all the “nonrandom” information in x just by saying that x belongs that S.)
Intuitively, Soph(x) is the length of the shortest computer program that describes, not necessarily x itself, but a set S of which x is a “random” or “generic” member. To illustrate, any string x with small Kolmogorov complexity has small sophistication, since we can let S be the singleton set {x}. However, a uniformly-random string also has small sophistication, since we can let S be the set {0,1}n of all n-bit strings. In fact, the question arises of whether there are any sophisticated strings! Apparently, after Kolmogorov raised this question in the early 1980s, it was answered in the affirmative by Alexander Shen (for more, see this paper by Gács, Tromp, and Vitányi). The construction is via a diagonalization argument that’s a bit too complicated to fit in this blog post.
But what does any of this have to do with coffee cups? Well, at first glance, sophistication seems to have exactly the properties that we were looking for in a “complextropy” measure: it’s small for both simple strings and uniformly random strings, but large for strings in a weird third category of “neither simple nor random.” Unfortunately, as we defined it above, sophistication still doesn’t do the job. For deterministic systems, the problem is the same as the one pointed out earlier for Kolmogorov complexity: we can always describe the system’s state after t time steps by specifying the initial state, the transition rule, and t. Therefore the sophistication can never exceed log(t)+c. Even for probabilistic systems, though, we can specify the set S(t) of all possible states after t time steps by specifying the initial state, the probabilistic transition rule, and t. And, at least assuming that the probability distribution over S(t) is uniform, by a simple counting argument the state after t steps will almost always be a “generic” element of S(t). So again, the sophistication will almost never exceed log(t)+c. (If the distribution over S(t) is nonuniform, then some technical further arguments are needed, which I omit.)
How can we fix this problem? I think the key is to bring computational resource bounds into the picture. (We already saw a hint of this in the discussion of entropy.) In particular, suppose we define the complextropy of an n-bit string x to be something like the following:
the number of bits in the shortest computer program that runs in n log(n) time, and that outputs a nearly-uniform sample from a set S such that (i) x∈S, and (ii) any computer program that outputs x in n log(n) time, given an oracle that provides independent, uniform samples from S, has at least log2(|S|)-c bits, for some constant c.
Here n log(n) is just intended as a concrete example of a complexity bound: one could replace it with some other time bound, or a restriction to (say) constant-depth circuits or some other weak model of computation. The motivation for the definition is that we want some “complextropy” measure that will assign a value close to 0 to the first and third coffee cups in the picture, but a large value to the second coffee cup. And thus we consider the length of the shortest efficient computer program that outputs, not necessarily the target string x itself, but a sample from a probability distribution D such that x is not efficiently compressible with respect to D. (In other words, x looks to any efficient algorithm like a “random” or “generic” sample from D.)
Note that it’s essential for this definition that we imposed a computational efficiency requirement in two places: on the sampling algorithm, and also on the algorithm that reconstructs x given the sampling oracle. Without the first efficiency constraint, the complextropy could never exceed log(t)+c by the previous argument. Meanwhile, without the second efficiency constraint, the complextropy would increase, but then it would probably keep right on increasing, for the following reason: a time-bounded sampling algorithm wouldn’t be able to sample from exactly the right set S, only a reasonable facsimile thereof, and a reconstruction algorithm with unlimited time could probably then use special properties of the target string x to reconstruct x with fewer than log2(|S|)-c bits.
But as long as we remember to put computational efficiency requirements on both algorithms, I conjecture that the complextropy will satisfy the “First Law of Complexodynamics,” exhibiting exactly the behavior that Sean wants: small for the initial state, large for intermediate states, then small again once the mixing has finished. I don’t yet know how to prove this conjecture. But crucially, it’s not a hopelessly open-ended question that one tosses out just to show how wide-ranging one’s thoughts are, but a relatively-bounded question about which actual theorems could be proved and actual papers published.
If you want to do so, the first step will be to “instantiate” everything I said above with a particular model system and particular resource constraints. One good choice could be a discretized “coffee cup,” consisting of a 2D array of black and white pixels (the “coffee” and “milk”), which are initially in separated components and then subject to random nearest-neighbor mixing dynamics. (E.g., at each time step, we pick an adjacent coffee pixel and milk pixel uniformly at random, and swap the two.) Can we show that for such a system, the complextropy becomes large at intermediate times (intuitively, because of the need to specify the irregular boundaries between the regions of all-black pixels, all-white pixels, and mixed black-and-white pixels)?
One could try to show such a statement either theoretically or empirically. Theoretically, I have no idea where to begin in proving it, despite a clear intuition that such a statement should hold: let me toss it out as a wonderful (I think) open problem! At an empirical level, one could simply try to plot the complextropy in some simulated system, like the discrete coffee cup, and show that it has the predicted small-large-small behavior. One obvious difficulty here is that the complextropy, under any definition like the one I gave, is almost certainly going to be intractable to compute or even approximate. However, one could try to get around that problem the same way many others have, in empirical research inspired by Kolmogorov complexity: namely, by using something you can compute (e.g., the size of a gzip compressed file) as a rough-and-ready substitute for something you can’t compute (e.g., the Kolmogorov complexity K(x)). In the interest of a full disclosure, a wonderful MIT undergrad, Lauren Oullette, recently started a research project with me where she’s trying to do exactly that. So hopefully, by the end of the semester, we’ll be able to answer Sean’s question at least at a physics level of rigor! Answering the question at a math/CS level of rigor could take a while longer.
PS (unrelated). Are neutrinos traveling faster than light? See this xkcd strip (which does what I was trying to do in the Deolalikar affair, but better).
 Follow
Follow
Comment #1 September 23rd, 2011 at 2:23 pm
What about Logical Depth, as defined by Charles H. Bennett (see http://en.wikipedia.org/wiki/Logical_depth and http://bit.ly/nh0bra for more details)? It seems to me that it is also a good proxy for complexity.
Comment #2 September 23rd, 2011 at 2:44 pm
As you demonstrate, the first law of complexodynamics is: complexity is inversely proportional to reason. This is also known as the KISS rule: Keep It Simple, Stupid.
OF COURSE complexity/interestingness peaks in the middle of an evolution, because that’s when the system is EVOLVING. Complexity/interestingness is maximized when things are changing. Initial state: delta = 0, boring. Final state: equilibrium, boring. Intermediate states: that’s where all the interesting stuff is happening. The monotonic Second Law is the same thing as the monotonic passage of time. Entropy only reaches its maximum, and complexity/interestingness returns to its minimum, when time stops and all evolutions are static. See the coffee cup slide.
Comment #3 September 23rd, 2011 at 2:55 pm
Consider the 2^n state space of some 3SAT equation, where each vector represents either {satisfiable, not satisfiable}. Take a 3SAT instance which maximizes the complextropy of such state space (over all state spaces of 3SAT instances). Maybe this could be useful to prove some lower bounds on SAT.
Comment #4 September 23rd, 2011 at 2:56 pm
Fascinating stuff, Scott! I wonder if strings of human language would fall into the “high-complextropy” category. It would be interesting to test this empirically once a good model is developed.
Comment #5 September 23rd, 2011 at 3:49 pm
Complexodynamics #2:
OF COURSE complexity/interestingness peaks in the middle of an evolution, because that’s when the system is EVOLVING.
Yeah, I completely agree that that’s the intuition! The hard part is to come up with some formal, quantitative measure of “complexity/interestingness” that matches that intuition. When you actually try to do that, you run into lots of issues that I don’t think are nearly as obvious, and which are what this post was about.
Comment #6 September 23rd, 2011 at 3:49 pm
Thanks for the plug, Scott! And thanks even more for thinking about the problem. (Although now I’ll have to do a less-superficial job on the blog post I was planning myself…)
I’ll certainly need to think more carefully about the careful definitions you’ve suggested, although we’re certainly thinking along similar lines. (I even thought of using file-compression algorithms.) It would definitely be fun to have an actual argument for a clearly-stated principle.
There does seem to be one difference of approach that may or may not be important. Namely, I’m convinced of the importance of coarse-graining, which you don’t seem to bring into play at all. Note that I did actually propose an (admittedly informal) definition of “complexity” on slide 15:
http://www.slideshare.net/seanmcarroll/setting-time-aright
Namely, “the Kolmogorov complexity of the description of each *macrostate* of the system.”
Obviously that relies on a fixed coarse-graining supplied ahead of time, to partition the state space into macrostate equivalence classes. This makes some people nervous because it seems arbitrary, but to me it’s both legitimate and crucial (at least I suspect so). In the real world, we can stare as much as we want at that class of cream and coffee — we’re not going to end up specifying the microstate by measuring the position and momentum of every single molecule. Our eyes just don’t work that way. We have available only certain macroscopic features of the system, and that is ultimately where the coarse-graining comes from.
That may or may not be a minor point, I’m not sure. Certainly the most interesting questions are the ones you identified, to which I have no good answers — in what way does complexity develop, at what speeds, etc.
Comment #7 September 23rd, 2011 at 3:52 pm
Actually I should say two more things.
First, while “Complexodynamics” is certainly right that there’s a sense in which complexity must go up and then down in this case, it’s far from clear how much it goes up and in what way. In the coffee cup, we could imagine completely uniform diffusion, which would keep the complexity pretty low. In fact, that probably happens in an isolated coffee cup; for this picture I reached in and poked it with a spoon. But there are other systems in which the complexity goes up appreciably, like the universe. Any would-be law better handle this difference.
Second, Raissa D’Souza (who studies real-world complex networks) pointed out to me at the conference that it’s likely that an honest graph of complexity vs. time isn’t nearly that smooth, as complexity can grow and then crash and grow again. Something else that a proper law of nature better be able to accommodate.
Comment #8 September 23rd, 2011 at 3:59 pm
Thanks, Sean! The difficulty is that I couldn’t figure out how to formalize the concept of a “macrostate” in any satisfactory way. However, I completely agree that one needs, if not that concept itself, then something else that plays the same role (since otherwise the entropy will essentially never go up, as I said in the post)! In my definition, the restriction to efficient sampling algorithms is what plays the role that coarse-graining might play in a more physics-based argument (i.e., it’s the thing that prevents us from saying that the entropy is small because of detailed regularities in the microstate that no one could ever notice in practice).
Comment #9 September 23rd, 2011 at 4:13 pm
Alejandro Weinstein #1:
What about Logical Depth, as defined by Charles H. Bennett
Great question! I’ve been extremely interested in Bennett’s logical depth measure for a while, and I considered discussing it in the post, ultimately deciding against.
The bottom line is that I think logical depth is not the right measure for this job, because in contrast to sophistication, I don’t see any intuitive reason why the depth should become large at intermediate times in (say) the coffee cup example!
Recall that the logical depth of a string x is (essentially) the number of time steps taken by the shortest program that outputs x. Now, to describe the state of a coffee cup with little tendrils of milk that are developing in some probabilistic way, it seems to me that we want to describe the boundaries of the all-milk region, the all-coffee region, and the regions with various mixtures of the two. Once we’ve specified those boundaries, an algorithm can output a microstate for the coffee cup that’s macroscopically indistinguishable from the observed one, by sampling coffee elements with independent probability p and milk elements with probability 1-p in those regions that have been specified to have a (p,1-p) mixture.
Now, the above will probably be a sophisticated/complextropic description in the sense of my post, since specifying the boundaries of the milk tendrils might require many bits. But it won’t be a deep description: once you’ve specified the boundaries, actually sampling a microstate can be done in nearly-linear time! Therefore the depth need not become large at any point during the mixing.
If the above argument is wrong, I’ll be extremely grateful to anyone who can explain why.
Comment #10 September 23rd, 2011 at 4:28 pm
I think this is a case of selection bias. We pay attention to emergent complex phenomena and give them a name. We name stars, not amorphous dust clouds. We notice galaxies, not diffuse intergalactic gas. We notice the cloud that looks like a duck. Some processes produce complexity, some don’t. We just get interested in the ones that do.
Entropy always wins in the end, so eventually the emergent complex system decays.
It’s not so clear that there’s anything to explain.
@Sean – Isn’t your coarse-graining the same as Scott’s definition of S – the least complex set within which x is effectively random?
Comment #11 September 23rd, 2011 at 4:37 pm
Re: Scott #9:
I’m not sure I understand your argument correctly, but couldn’t also the configuration/arrangement of the mixed boundaries be itself logically deep? There could be a huge number of different (p_i,1 – p_i)’s in the mixing zone, and the shortest sampling program might require extra time that’s dependent on the number of different mixing zones.
Comment #12 September 23rd, 2011 at 4:41 pm
“Foster Boondoggle” #10: What’s interesting is that, in denying that there’s anything to explain, you threw around phrases like “emergent complex system,” simply assuming that people would know what’s meant by them! But, as I tried to explain in the post, defining those concepts rigorously enough that we can prove theorems about them is the main challenge here!
To put it differently: can you write a computer program that takes as input a raw bit string, and that decides whether or not that string encodes “emergent complex behavior”? How do you do it?
The task might sound hopeless, but in the post I proposed a class of programs to do exactly that: namely, programs that calculate the “complextropy” as defined in terms of resource-bounded Kolmogorov complexity. You’re more than welcome to criticize my proposal or suggest a better one, but you can’t do so while blithely using words for which the entire problem is to define those words! 😀
Comment #13 September 23rd, 2011 at 4:46 pm
Henry #11: Yes, it’s possible that the logical depth could become large at intermediate times, or that it could do so in some model systems / cellular automata but not in others. I just don’t see an inherent reason for that to happen: if it did happen, it would seem almost like an accident! Maybe I’m wrong though.
Comment #14 September 23rd, 2011 at 6:16 pm
Interesting article, Scott. But I must say I’m surprised you attended such a fantastically self-indulgent conference as Setting Time Aright. Even though it seems to have been somewhat fruitful for you, the monumental waste and extravagance of such an enterprise should be deeply repugnant to any morally sophisticated person–which I have always considered you to be.
Comment #15 September 23rd, 2011 at 6:35 pm
“Sampson Brass” #14:
the monumental waste and extravagance of such an enterprise should be deeply repugnant to any morally sophisticated person
WTF? It’s not like any public money was spent on this—just FQXi’s (i.e., the Templeton Foundation’s). If they want to pay to send me on a nice cruise, I’m morally obligated to say no? Can you explain why?
Comment #16 September 23rd, 2011 at 6:56 pm
Gee, Scott, I just meant that regardless of where the money came from, it shouldn’t have been spent as it was, on a luxurious cruise through waters far from the homes of many of the participants. Sort of like how an argument can be made that it is immoral (irrespective of all other factors) for a rich person to spend his or her own money on, say, a $500,000 automobile. We’re talking about indulgence, waste, extravagance; I don’t see how that can be justified in a world where so many people have so little. Though for the record I’ll bet the cruise was a lot of fun and I’m not sure I would have had the moral courage to refuse an invitation had it been tendered me!
Comment #17 September 23rd, 2011 at 7:24 pm
One (very simple) way to think about the notion of “coarseness” in the coffee example would be to look at all possible scales. For each size parameter, divide the cup into cubes of that size, and average the milk-coffee content in each cube. Now look at the time vs Kolmogorov complexity graph for the “pixellated” cup of coffee that you get at this scale. At very small scale, the graph will be the increase in entropy from the 2nd law of thermodynamic (assuming that the process is randomized, or assuming that the process is in some sense pseudorandom and that we are using time-bounded Kolmogorov complexity); at a scale large enough that the cup is a single cell, the Kolmogorov complexity is constant.
If you consider the whole 3-dimensional scale-time-complexity graph, however, there will be some “bump” at middle scales.
I don’t know what would be good computational definitions that would allow a more abstract treatment in which one would see the same qualitative phenomenon.
Notion of samplability and distinguishability seem related enough: if, after averaging over a certain scale, you have small descriptive complexity, then you have a sampler that, in each cell, will simply produce a random mix of coffee and milk according to the relative density, and this will be indistinguishable from “reality” by an observer that is not able to resolve what happens within cells.
Comment #18 September 23rd, 2011 at 7:31 pm
Sampson #16:
Except that, uhh, the “far from the homes of many of the participants” part is no different than any academic conference anywhere! By the triangle inequality, you can’t have an international conference without it being far from someone‘s home… 🙂 Furthermore, only 2 out of 6 nights were spent on the ship, and I really doubt that this conference was significantly more expensive than an ordinary conference in a hotel (those are quite expensive as well). And the ship was the National Geographic Explorer, which is not exactly a typical luxury ship.
So, I think it boils to a question raised in the Ask Me Anything post: should all academic conferences should be cancelled? But if so, why start with academic conferences? Wouldn’t it be better first to request a halt to ordinary vacations?
Incidentally, this happens to have been the first time in my life on a cruise of any kind. I’ve never been to the Caribbean or Hawaii, and in fact I haven’t gotten on a plane “purely” for vacation purposes in the last decade. Can you say the same? How much money do you spend on “extravagances”? However much it is, shame on you! 😉
Comment #19 September 23rd, 2011 at 7:42 pm
Hi Scott – I didn’t mean to dis your post. I found it quite interesting. But I was responding to the opening question: “why does ‘complexity’ or ‘interestingness’ of physical systems seem to increase with time and then hit a maximum and decrease?” My point was just that it’s only those systems that we study. For lots of other systems this wouldn’t be true.
Take your cellular automata test case, except instead of using an updating rule that leads to simple diffusion, randomize also over the rules and initial states. Most of those systems will be utterly boring – e.g., all the black pixels will disappear, or the system will remain chaotic and random at all times. We won’t talk about them because there’s nothing much to say. But one of the systems will be Conway’s Life, which will be initially chaotic, but then evolve through some interesting intermediate state with gliders and perhaps other more complicated structures, before eventually settling down to blinkers, blocks and other entropic debris. That’s the system we pay attention to.
Responding to the opening question: it’s not true in general. It is for some small subset of dynamical systems and initial conditions, and those are the ones we talk about.
Comment #20 September 23rd, 2011 at 7:55 pm
Scott,
Re: Samson
Don’t even bother trying to defend this to someone who’s obviously not ever going to accept it. What’s the point?
If Samson feels so strongly about this type of thing, he can certainty make sure he never does anything so morally corrupt.
And, if it’s really a problem for him, he can stop following your blog and spend his valuable time dong something else.
What is this guy? A monk?
Have some fun, relax, be creative and continue to come up with great things, which you seem to have a knack for
By the way, I hope this was a family affair, although I know it’s hard to organize this sometimes.
Comment #21 September 23rd, 2011 at 7:56 pm
I have to back Sampson up on this one, I’m afraid. We didn’t make it public, but the invited speakers were treated to lavish caviar breakfasts and complementary between-session footrubs. Which was fine, but I thought the hot and cold running champagne was a bit morally reprehensible.
Also, Scott, I notice that you have a tendency to tell “jokes” during your talks. This squanders valuable time that could be used to convey information rather than simply being enjoyable, and furthers your reputation as a moral monster. And here I thought better of you.
Comment #22 September 23rd, 2011 at 7:59 pm
Foster #19: I agree that there are plenty of systems that never do anything “complex” or “interesting,” no matter how long you let them run. On the other hand, this is a rare case where I might need to side with Wolfram 🙂 : it seems to me that “complex behavior” is the rule rather than the exception. Crucially, in using the word “complex” here I don’t mean anything as grand as life or intelligence: all I mean is behavior (like that of Sean’s second coffee photo) that doesn’t manifestly fall into one of the two categories of
(1) simple and predictable or
(2) completely entropic and random.
You mention that “most” cellular automaton rules lead to something boring, but it seems to me that that’s an artifact of restricting the search space to a tiny set of rules (e.g., 1-dimensional, 2-state, nearest-neighbor). As you increase any of those parameters—e.g., the number of colors per pixel—I conjecture that the “interesting” rules will come to asymptotically dominate, and moreover that they’ll do so extremely quickly. It would be great to prove that, if it hasn’t been done already.
Comment #23 September 23rd, 2011 at 8:22 pm
Foster,
As you you seem to be hinting (and thinking), the question is implicitly anthropic. That is, as observing participants in this universe, we find that the universe evolves this way because, if it didn’t, we never would have been part of it. To the extent that we imagine ourselves as external observers, we still find only this kind of universe worth talking about, because it is complex enough to accommodate us as observing participants (actively observing subsystems). That is, it resembles the universe in which we actually find ourselves, and which manifestly sustains our existence, at least for a while.
That sounds like another attempt to write off the question as mostly vacuous, but I have something else in mind. Such a universe is one in which we can think and do science. That is, for a significant period of time it sustains that peculiar combination of stability (reproducibility) and dynamism (and diversity) in which it makes sense to pose scientific questions and attempt to answer them. In particular, it prompts us—again, as participating subsystems—to seek stability and invariant patterns amidst and underlying change, and gives us some hope of identifying them before the clock runs out on our species.
Comment #24 September 23rd, 2011 at 8:37 pm
[PS: Is there a Godwin’s Law for allusions to the Anthropic Principle? 🙂 ]
Comment #25 September 23rd, 2011 at 8:50 pm
Scott’s conjecture in #22 that “interesting” rules asymptotically dominate as CA algorithms become more complex is extremely interesting, if true. I actually don’t even have an intuition either way. Does anyone think something along those lines could be provable?
Comment #26 September 23rd, 2011 at 9:18 pm
I know this isn’t the central issue, but as background for computer scientists, it would be very nice to have a precise formulation of the 2nd Law *as a statement about Cellular Automaton behavior*, as well as some sense of its scope.
For which CA rules/initial states does it hold true? is the Law provable? Is it ultimately a tautology, or not? Are we discussing a single notion of “macro-states”/”coarse-graining”/”pixellation”, or allowing for a more abstract setting? And so on.
I’ve read a few web pieces by Wolfram and others on this issue, but none that satisfy me. Can anyone help out?
Comment #27 September 23rd, 2011 at 9:31 pm
Like all life, we harvest energy from entropy gradients. This may be why the middle glass is most interesting to us. We can’t do anything with the glass on the right, so there’s no need to pay attention to it. The glass on the left is easy – I can shake it and generate electricity. But competition for such easy gradients pushes us to ever harder ones, and we evolved reward systems to help us.
This suggests invoking something like Landauer’s principle. Define complextropy for dynamic systems sampled in time. At each sample, observe the system and predict its next state. The bits you get right are counted toward your booty. Run your algorithm for free but in place, so you spend energy resetting registers and so forth. Complextropy could be t/(b-c), where b is the number of bits in your booty, c is the number you erased (energy cost), and t the number of samples. It will be negative for the glass on the right, small for the glass on the left, and large for the glass in the middle. Buy as much memory as you like for best performance, as long as it is small compared to b.
There may be a way to extend this to static examples like an *image* of a coffee cup. But starting from such examples may be trappy. They look interesting, perhaps only because we’ve learned to quickly recognize the dynamic systems they’re part of.
Comment #28 September 23rd, 2011 at 9:36 pm
Let P(c|r) be the probability density of color c at position r. \sum_c P(c|r) = 1. Let \mu([a,b]) = b-a. Generalize \mu(.) to a proper measure.
Can’t you use the following non-sophisticated measure of sophistication?
\mu( range(P(c|r)) )
(it’s zero initially and finally but not in between. You can average over all positions r if you want a bulk measure )
Comment #29 September 23rd, 2011 at 9:39 pm
Addendum: by range(.), I meant the range of the function P(.|r) over all c at fixed r
Comment #30 September 23rd, 2011 at 9:59 pm
Since no one has opened this can of worms, I’ll make the first neutrino comment.
I don’t think the situation is as analogous to the Deolalikar case as people would think. I think this is actually far more probable of being valid (not that I am saying anything about how absolutely likely or not it is that it is valid). The first reason, is that you can’t ignore the fact that it is a post five sigma result, hell it’s post six sigma. Now, that doesn’t mean there’s not some unseen systematic errors, but these guys seem to be pretty good at what they do, and it appears that they have been working their asses off trying to find any potential systematic errors. In their arXiv paper they are careful to never use evocative “superluminal” language and express an extremely conservative viewpoint on the matter. Again, this doesn’t mean it’s not a systematic error, but if it is it would have to be slipping by a large number of very skeptical skilled professionals that are actively and sincerely hunting for it.
The next thing is that contrary to the popsci (and even some legit sci) word floating around, this does not violate SR! SR works fine with superluminal particles, but they open the possibility of retrocasual signals and either the mass must become imaginary OR both the energy and momentum must become imaginary. All of these things seem ridiculous, but given some of the radical revolutions physics has seen, its not entirely out of the question. Even with superluminal particles, retrocasual signals could end up being restricted in other ways, or perhaps a new picture of causality would be needed. In fact, there is already some theory results out there that show certain tachyons can’t be used to signal FTL.
Of the other implications the least ridiculous (though still ridiculous) of these is the imaginary mass, or negative mass squared. Coincidentally or not, negative values for the mass squared of the neutrino were measured multiple independent times over a decade ago! In fact it seemed like everyone that tried measuring the square mass of the neutrino found it to be negative. The first of these cases had a lot of noise, but I believe some of the results eventual got to a few sigma. For some elusive reason that no one seems to know, no fuss was ever made over the results. It sparked some theoretical papers on superluminal neutrino models, but overall it faded away. Even the critics of the Opera result note these old results and admit that they can’t come up with a dismissal any better than “well we stopped hearing about it so it was probably nothing”.
On top of all this, their have been level headed people arguing that neutrinos are tachyonic for over 20 years, and there are a number of reasons why they did so. Furthermore, there is nothing in any law of physics directly forbidding tachyons as far as I know. The only things that do are the result of a number of dearly held intuitions being forced upon the laws of physics. And if the last century has taught us anything, it is that we shouldn’t get too cozy with our deepest intuitions.
Keep your hand on your wallet, but be ready to take your credit card out if the time comes.
Comment #31 September 23rd, 2011 at 10:03 pm
To the extent that this is a “why” question, and not merely a matter of formally characterizing the complexity of the “middle” state, what about the role of gravity? After all, isn’t it the universal attraction of gravity, including the expansion of the universe as described in general relativity, that drives primordial matter towards this complicated non-equilibrium state? I’m surprised Sean Carroll didn’t bring this up.
Comment #32 September 23rd, 2011 at 10:03 pm
rrtucci: Thanks for the interesting suggestion! However,
(1) Won’t μ(range(P(c|r))) always be 0 in a discrete system like the one we’re considering, since there are only finitely many c’s and r’s, hence finitely many P(c|r)’s?
(I agree that one could easily fix this problem, for example by coarse-graining over the unit interval.)
(2) Your measure only makes sense given a probability measure over the microstates. However, I want a complextropy measure that (at least in principle) can be calculated for a specific microstate, and (a related requirement) makes sense even for deterministic dynamical systems. That was my motivation for bringing in Kolmogorov complexity. (Sorry I didn’t make that more explicit in the post!)
(3) Your measure is (of course) rather tailored to the coffee cup example, and could be invalidated even by small changes to that example. For example, suppose I told you that there were equal amounts of coffee and milk, and that with probability 1/2 the milk started out on top of the coffee, and with probability 1/2 the coffee started out on top of the milk. In that case, symmetry considerations imply that P(c|r) would always be 1/2, for every c and r and at every time step. Yet it still seems intuitively like the complextropy starts out small, increases, and then decreases again.
Comment #33 September 23rd, 2011 at 10:11 pm
PS: I should have said “…, along with the expansion of the universe as described in general relativity, …”.
Comment #34 September 23rd, 2011 at 10:25 pm
Justin #30: I agree with almost everything you say (as usual, Sean Carroll did a great job summarizing the issues). But of course, during the Deolalikar affair, there were also lots of serious people making serious arguments for taking that claim seriously! It was only long experience with wrong P≠NP proofs that emboldened me to bet against.
As for the neutrinos, I’m obviously far from an expert, but am moved by the following two points:
(1) Closed timelike curves seem to me to be a different order of strangeness from anything thus far discovered in physics—like maybe 1000 times stranger than relativity, QM, virtual particles, and black holes put together. And I don’t understand how one could have tachyonic neutrinos without getting CTCs as well—would anyone who accepts that possibility be kind enough to explain it to me?
(2) As I understand it, the possibility of systematic errors in an experiment of this sort are legion, no matter how careful the experimenters are. And if there is a systematic error, then presumably there’s a 50% chance that it’s going to be in the direction that was reported! In other words: once someone decides to search for particles going ~1+10-5 times faster than the speed of light, the prior probability that they’ll find what look like such particles seems to me to be quite high, even under the assumption that no such particles exist.
Comment #35 September 23rd, 2011 at 10:48 pm
“In answering Sean’s provocative question (whether there’s some “law of complexodynamics” that would explain his graph)”
I’m gonna side with [Complexodynamics: Comment #2] here, as in:
Yeah, it’s called “Rolle’s Theorem”:
In calculus, Rolle’s theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative (the slope of the tangent line to the graph of the function) is zero.
Comment #36 September 23rd, 2011 at 10:57 pm
IThinkImClever: Your argument is “clever” but wrong! The constant zero function would also satisfy Rolle’s Theorem. Therefore, that theorem is manifestly irrelevant to the problem that I stated: explaining mathematically why the complextropy becomes large and positive at intermediate times.
Comment #37 September 24th, 2011 at 12:12 am
Justin: I’m no physicist and I haven’t read the results about negative squared mass of neutrinos, so I’m quite underqualified to comment, but:
I’m quite skeptical about the negative squared mass claims, because how would one even set up an experiment to measure imaginary mass? The caricatured method that comes to mind is this: measure the velocity of neutrino, plug in velocity into relativistic Lorentz equations, and “observe” imaginary mass! Please let me know if this resembles the actual experiments at all.
If the actual experiment were anything like this, then I believe we would have the same questions about the method of measuring velocities of neutrinos.
Then, it would be hard to say that the results of the imaginary mass experiment support the results of FTL neutrino experiment, because the former relies on the latter!
(Apologies for diverting comment thread from “complextropy”!)
Comment #38 September 24th, 2011 at 1:44 am
Seems at least one physicist has had the same idea as you!
Chang Kee Jung, a neutrino physicist at Stony Brook University in New York, says he’d wager that the result is the product of a systematic error. “I wouldn’t bet my wife and kids because they’d get mad,” he says. “But I’d bet my house.”
(Hat tip to hegemonicon on LessWrong.)
Comment #39 September 24th, 2011 at 1:46 am
(I guess not really, as I don’t see anywhere where he’s announced that he actually *is* betting his house, and stated terms. But someone was going to say it. 🙂 )
Comment #40 September 24th, 2011 at 2:41 am
@Scott: Comment #36
OK, fine.
But note that I claimed only to ever be clever, and not right. 😉
Also, I won’t maintain here that the constant zero function case would actually cause the question to be trivial and uninteresting. 🙁
Anyhow, after thinking about “complextropy” a bit more, I am now wondering:
1) Why are we assuming that “equilibrium is simple”, when the length of the *minimum boolean expression* required to describe the ‘mixing’ system *exactly* at time step t grows rapidly as entropy increases?
(BTW, how about these minimum boolean expressions as an objective, calculable criterion for “complextropy”, on say, your 2D array of black and white pixels?)
2) In terms of universality (of whose threshold of acquirement is extremely low), once acquired by, or present in a system, where is there left to go? What is more ‘complex’ than a ‘universal computer’ on which these ‘particles’ are interacting on? Aren’t we ‘maxed out’ pretty early on in the game?
3) Perhaps we need better definitions of the ‘players’ involved, especially physical ‘randomness’? Maybe, in the end, only pseudorandomness really exists, if indeed the universe is ultimately discrete at the lowest level, and everything has low Kolmogorov complexity.
*As an aside, on the Neutrino Debacle: Yeah, again, time to again first invoke the KISS Principle and/or Murphy’s Law. It’s most likely a simple error.
Comment #41 September 24th, 2011 at 2:57 am
w.r.t the Neutrino Debacle: I would now be cautious to taking a betting position against “superluminal neutrinos”, but ONLY because Nikola Tesla somewhat foresaw it, and Tesla was NEVER wrong. 😀
“In 1901 Nikola Tesla was one the first to identify “radiant energy.” Tesla says that the source of this energy is our Sun. He concluded that the Sun emits small particles, each carrying so small of a charge, that they move with great velocity, exceeding that of light. Tesla further states that these particles are the neutron particles. Tesla believed that these neutron particles were responsible for all radioactive reactions. Radiant matter is in tune with these neutron particles. Radiant matter is simply a re-transmitter of energy from one state to another.”
“All of my investigations seem to point to the conclusion that they are small particles, each carrying so small a charge that we are justified in calling them neutrons. They move with great velocity, exceeding that of light. More than 25 years ago I began my efforts to harness the cosmic rays and I can now state that I have succeeded in operating a motive device by means of them. I will tell you in the most general way, the cosmic ray ionizes the air, setting free many charges ions and electrons. These charges are captured in a condenser which is made to discharge through the circuit of the motor. I have hopes of building my motor on a large scale, but circumstances have not been favorable to carrying out my plan.”
Comment #42 September 24th, 2011 at 9:00 am
Just a sentence or two about neutrinos. Even if neutrinos are tachyonic, you still have to explain why they aren’t traveling at speeds closer to the speed of light, given their low mass. To me, the really unlikely thing about this measurement is the magnitude of (v_neutrino – speed of light), though I’ll admit that the sign is weird too.
Comment #43 September 24th, 2011 at 2:35 pm
This topic has fascinated me for years, and I’m convinced (intuitively) that it will remain an open-ended problem.
I was going to suggest the evolutionary, and then the anthropological aspect, but I see others here already have.
This leaves the “Edge of Chaos” aspect, which may help round out your research.
1993—Melanie Mitchell & James Crutchfield & Peter Hraber—Dynamics, Computation, and the “Edge of Chaos”: A Re-Examination http://www.santafe.edu/research/working-papers/abstract/e5b0ef2ae9887b454ea8501f4a9568a7/
2010—Thierry Mora & William Bialek—Are biological systems poised at criticality? http://arxiv.org/abs/1012.2242
I believe the Kolmogorov-based approach is a dead end, as we inherently lack the necessary context within the vast space of possible evolutionary trajectories to predict which mathematical combinations will represent synergistic and persistent, thus “interestingly complex” novel structures.
As to the anthropological question of why *we* find certain structures “interestingly complex”, I believe this is doable in theory, and to the extent it is achievable it could provide a useful building-block for comparative modeling of systems of values and ethics.
Comment #44 September 24th, 2011 at 2:57 pm
I started to comment on Scott’s CTC worry, but it turned into a blog post:
http://blogs.discovermagazine.com/cosmicvariance/2011/09/24/can-neutrinos-kill-their-own-grandfathers/
Comment #45 September 24th, 2011 at 4:07 pm
@Justin Dove: Despite the fact that superluminal signalling may not be possible for certain classes of tachyons, from what I understand, if the result is correct, superluminal signalling shouldn’t be that hard – the 0 bit could be represented as a small number of neutrinos being sent (and detected) while the 1 bit could be a much larger number of neutrinos being sent (and detected). Varying this, one should be able to send superluminal messages.
Comment #46 September 24th, 2011 at 4:12 pm
Jef Allbright #43:
I believe the Kolmogorov-based approach is a dead end, as we inherently lack the necessary context within the vast space of possible evolutionary trajectories to predict which mathematical combinations will represent synergistic and persistent, thus “interestingly complex” novel structures.
Look, there’s clearly the issue that, while the second coffee cup in Sean’s picture is more “interesting” than the first or third cups, it’s still not very interesting! (No offense, Sean.)
So it would be nice to have a complextropy/interestingness measure that assigned an even higher score to, for example, the coffee being drunk by a baboon wearing a top-hat.
However, I took at as obvious that the goal here was not to construct an “ultimate theory of interestingness” in one go—yes, I agree, that sounds pretty hopeless!—but merely to do somewhat better than entropy as an interestingness criterion, by matching our intuition that the second cup is more interesting than either the first or the third. I should have made that clearer in the post.
Comment #47 September 24th, 2011 at 4:35 pm
(Why are people talking about neutrinos in response to a post that’s not at all about neutrinos?)
I’ve decided to cast my vote for the “logical depth” version. Assume we have some finite system evolving according to some rules. If the system has a simple initial state, and if the rules are “interesting”, and if the system’s rules don’t discard information, then the logical depth will tend to increase linearly at first: the shortest description of the current state will be to give the initial state and the amount of time that’s passed. However, after a long time (on the order of the number of possible states of the system, in the worst case), it will no longer be worth it to describe the state via the entire history. At this point the logical depth will at least hit a ceiling. Again assuming the rules are sufficiently “interesting”, the logical depth will drop back down to near 0, because at this stage the system state will look random (and that’ll be it’s shortest description).
A word on my assumptions.
First, the assumption that we don’t discard information. I make this assumption because it’s needed for thermodynamics in the first place: if information ever went away, entropy could decrease. I think it’s also needed for my result here.
The relevant definition of “interesting” may sound like a sticking point. Intuitively, I mean that as the state evolves, it doesn’t stay simple. (The cream doesn’t stay at the top of the coffee, nor does it fall to the bottom in a straight line.) A decent definition for my purposes is that any state can reach a large portion of other states. (IE, for any initial state we choose, if we keep running the simulation for long enough, it will pass through at least 1/4 of the possible configurations– 1/4 being chosen arbitrarily). Since the vast majority of states have high kolmogorov complexity, this is enough to guarantee that the Kolmogorov complexity will increase over time and eventually hit the upper bound for the system, ie, the complexity of a randomly chosen configuration for that system. At this point the logical depth of a state will almost always be on the order of the log of the number of system states.
Will the logical depth exceed the log of the number of system states before that, though? I suspect so, because I suspect the best way to describe the system will be its history for a long time (on the order of the number of system states), and for as long as that’s the case, depth increases linearly. However, I’m not totally sure I can prove this based on my current definition of “interesting rules”. (They may not be interesting enough!)
Comment #48 September 24th, 2011 at 4:48 pm
This seems to me to be about coarse-graining, the picture of the cup on the left consists mostly of black and white pixels, neatly ordered.
The one in the middle is more interesting because it consists of mixed pixels of different colors, while the one on the right again has a simple description (all pixels are ‘brown’).
But of course the brown pixels hide the many possible microstates of black and white little drops. So the simple description (but with high entropy) is due to coarse-graining and ‘averaging’ of microstates.
So the question is why coarse-grained descriptions play such an important role and I would say the answer is that we human beings don’t care about the statistics of microstates but instead pay most attention to what our eyes report and they are coarse-graining in a particular way – optimized by evolution to make ‘important’ stuff interesting to us and boring stuff (=high entropy stuff) uninteresting to us.
Comment #49 September 24th, 2011 at 6:41 pm
@ comment #8 (& #48):
I think we don’t have to take the terms macro/micro too literally. Course-graining, to me, is about partial information. We can’t fully observe the state of the coffee, and a “macro-state” is just a set of states that we can’t distinguish from one another. So, to define entropy for deterministic systems, we make them partially observable. This is functionally similar to making them stochastic, since it means that we have uncertainty about the system.
Comment #50 September 24th, 2011 at 7:42 pm
There’s a really nice collection of work by Bill Bialek and collaborators on “predictive information” defined as “the mutual information between the past and the future of a time series.” In it they “argue that the divergent part of [the predictive information] provides the unique measure for the complexity of dynamics underlying a time series.”
This paper is very well written and, with a thorough discussion of its relation to previous work, is also a useful reference for those interested in these issues:
http://www.princeton.edu/~wbialek/our_papers/bnt_01a.pdf
Comment #51 September 24th, 2011 at 9:05 pm
@Henry The old experiments did *not* measure the mass in that way. They measured the mass squared “directly” using analysis of the beta spectrum of tritium decay. I’m not going to pretend to understand it completely, but there’s a large amount of literature and references at http://arxiv.org/pdf/0909.2104v1. The results were almost all (with a few exceptions) consistent with the possibility of positive mass squared values (within an error bar), but they nearly unanimously favored the negative side.
As time has gone on they have gotten closer to c, but oddly the absolute measurements are still often coming up negative. Now these results are not very interesting given the uncertainty, but the coincidence of the superluminal claims makes them fun to toy with at least.
@Scott I agree. The main difference I find with the Deolalikar situation is that this is a claim coming from a large group of people that *weren’t* looking for this, as far as I can tell (as opposed to one person that was). Furthermore, I’ve also read that they have spent months shaking their heads in disbelief and looking for systematic errors with the help of metrology folks. I get the impression that they had no intention of publicly announcing this, but ultimately it came to the point where they couldn’t find the error (if it exists) and needed to open it up to the peer community.
As far as CTC’s go, you could always go with Lorentz violations, but honestly I find that probably even more unappetizing. The other thing is to envoke some sort of consistency principle that forces ctc’s to only exist in consistent ways.
Again, I’m by no means claiming to believe this claim is true. But I just think its worth much more serious care and considerations then many other such incidents.
Comment #52 September 24th, 2011 at 10:31 pm
@Wolfgang may be on to something. If you look at the JPEG encoding (using DCT) of the image of the coffee, the less interesting cups have higher coefficients in the upper left and lower right of the DCT matrix. The interesting middle cup has lots more going on in the middle of the matrix. (You don’t get this effect with PNG or GIF images of coffee, so it may just be serendipity that Sean used JPEG.)
JPEG works by breaking an image into 8×8 pixel squares and doing a transformation that measures the visual complexity in the horizontal and vertical directions. The top left coefficient of the matrix is basically the average value of all the pixels and the bottom right a more or less checkerboard mix. From a distance, these two extremes both correspond to something that looks like gray. If you want interesting structure, you need stuff in the middle of the matrix.
Comment #53 September 25th, 2011 at 2:15 am
Scott @ 22, Sean Carroll @ 25:
I’d conjecture the opposite, that higher-dimensional (more complex rules because larger neighborhoods) spaces of CA rule sets have smaller subspaces containing “interesting” rules. If the “edge of chaos” is a real phenomenon (and there was some controversy about that the last time I looked), then it represents a hypersurface in the rule space around which “interesting” rules cluster, and that’s going to be a smaller percentage of the total space as the dimensionality increases.
In any case I rather doubt we’ll ever have a way to determine the complexity of a CA rule in less time than it takes to execute it; that would seem to violate the undecidability of the Halting Problem.
Comment #54 September 25th, 2011 at 2:49 am
Dear Scott, these are nice thoughts. Here are a few comments.
1) The idea that the complexity of a system increases in intermediate states is nice. Kolgomorov complexity appears to be much too complex notion of complexity to express this idea. Maybe some notions from ergodic theory (according to which both deterministic sequences and very simple random sequemces are “simple”) can be more relevant. (So perhaps “complex” should mean that the system does not behave deterministically; where by laws of large numbers simple random processes do behave deterministically.)
2) A related idea is that in physical systems, complex behavior is witnessed near criticality. Namely, if the system depending on some parameter t witnesses a phase transition for t=T_0 then it is considerably more “complex” when t is close to T_0.
3) There is some difficulty with the assertion that equilibrium states are “simple” with what we know about possible complexity of equilibrium states, be it in the context of quantum ground states, or in the context of protein folding.
It is not clear that we can usiversally claim that the equilibrium states must be “simple”.
4) One idea that I found appealing is that for certain purposes clocks of physical systems should be scaled in a way that the rate of time at a time T is inversly proportional to the “complexity” of the system at time T. So time passes slowly at interesting times and quickly at boring times.
Comment #55 September 25th, 2011 at 3:06 am
The difference between pictures 1,3 and 2 is the ability to predict color of the “cap”, based on their neighbors. The color distribution is almost everywhere uniform. In the “middle cap”, (I mean most interesting one) the knowledge of the “color” (say, some coding of possible configurations) for the “box” at any scale have no/minimal predictive power at distant “box” of the same scale, leading to situation similar to fractal images.
Comment #56 September 25th, 2011 at 4:57 am
There is, however, a difference between the Deolalikar affair and the current ftl neutrinos issue. The first one was original research claiming something groundbreaking, and attempting to supporting it in a scientific manner, even if the proof is not actually correct. The second is the case of the media trying to make news from a strange experimental result where the physicists apparently don’t claim to have found anything groundbreaking, which phenomenon is illustrated in the strip “http://www.phdcomics.com/comics/archive.php?comicid=1174”.
Comment #57 September 25th, 2011 at 11:01 am
I feel free to ignore the fact that it’s a “post six sigma result” because the number of sigmas is not a measure of reliability. It’s closer to a measure of how bad your initial assumptions are—not just the null hypothesis, but also anything regarding the experimental design. If it’s true that there are many possible systemic errors in the experiment (I’m nowhere near a physicist, so I can’t say), then that’s most likely what all those sigmas reflect.
Comment #58 September 25th, 2011 at 1:55 pm
For the record, I’ve long believed that there’s a similar argument to be made for an informational (or, in your language, complexodynamical) sweet spot in art. We don’t seem to derive a strong aesthetic response to paintings that are either too simple or too complex, because the former are boring and the latter are noise. There does seem to be a middle ground in which a painting contains the “right” amount of information.
Of course, any such measurement is tricky. If I turn the Mona Lisa upside down, or break it into 1″x1″ tiles and permute them, I have a design that’s very close in terms of information, but which may produce a quite different aesthetic response.
Of course, this is all pseudoscientific daydreaming until someone (not me) can produce a suitable mathematical definition, combined with a psychological validation. I will note that Jim Bumgardner did say something very similar in a short essay on information theory and art (http://www.mungbeing.com/issue_3.html?page=9#235), though using the language of Shannon entropy rather than Kolmogorov complexity.
Comment #59 September 25th, 2011 at 2:16 pm
Complexodynamics: While this is clearly an interesting direction, there is a major problem likely(?) to to prevent any useful results:
There is no reason to think there is ANY scalar (as opposed to multidimensional) function that meaningfully captures the notion of complexity (let along “interesting-ness”).
The situation is very different in thermodynamics, where entropy S has a reasonable, not arbitrary, definition. Key thermodynamic concepts are defined as derivatives of S, or with respect to S, and they agree with measurable quantities defining heat engines, etc.
Grasping for a workable definition of complexity seems rather like trying to define IQ.
Why discuss neutrinos right now? Well, because it would be a once in a century event. My (purely intuitive) estimate on the likelihood of this holding up: one in a million.
Comment #60 September 25th, 2011 at 5:11 pm
“Grasping for a workable definition of complexity seems rather like trying to define IQ.”
Yeah, I’m pretty sure Wolfram would have accomplished this, if at all possible, in his 20+ years and ‘million mouse miles’ of researching complexity for his tome, but I’m still rather happy with his book as an overall informal definition of this “Complexodynamics”.
Comment #61 September 25th, 2011 at 6:01 pm
Raoul #59: Once again, the key point is that I had no pretensions to define “complexity” for every possible purpose—only for the specific purpose of answering Sean’s question about the three coffee cups.
For some reason, many, many commenters seem to have missed that, and assumed that I was trying to do something much broader than I was.
Speaking of which, IThinkImClever #60: I’ve read Wolfram’s entire tome, and as far as I remember, he never once discusses the question of Sean that this post is about.
(More generally, Wolfram never offers any formal definition of complexity—his notion of complexity is analogous to Justice Potter Stewart’s “I know it when I see it” definition of pornography. His attitude toward people who try to formalize and prove things, as opposed just to eyeballing thousands of CA printouts, is one of open disdain.)
Comment #62 September 25th, 2011 at 7:13 pm
Well, as a quick response, I’d say that while Wolfram never focused on any *one* specific question in NKS, I think he did succeed in his overall general goal of elucidating the origins of complexity, and why it occurs at all.
And you’re right, in sections where he mentions definitions (e.g. Defining Complexity, pg.557), he only considers how it *might* be formally defined, given our limited processes of perception and analysis.
And while I wouldn’t ever have a disdain at formalizing and proving things, I am with Wolfram for now in just accepting as axiom that you never need to go beyond the elementary CA’s, as processes will only ever evolve behaviours that can be ‘captured’ by the 4 atomic/primitive patterns they exhibit: simple, repetitive, complex, random.
But that being said, I think your attempt at formalizing Sean’s question is quite clever, using the formally defined concept of Sophistication within Kolmogorov Complexity.
I think we all see what you are trying to get at, but of course we are naturally gonna go off on tangents. 🙂
Comment #63 September 25th, 2011 at 8:06 pm
IThinkI’mClever,
“Yeah, I’m pretty sure Wolfram would have accomplished this, if at all possible, in his 20+ years and ‘million mouse miles’ of researching complexity for his tome, . . .”
So, you’re saying it’s impossible because Wolfram hasn’t accomplished it, because it’s “impossible” — really, your “pretty sure” about all of this?
What is it do think went wrong; do the the laws of physics say it’s impossible? Or, is it that humans just aren’t bright enough to “really” figure it out?
And, if we haven’t, why is that, because if we had it would have been this guy Wolfram who would have manged to figured it out already?
What is it exactly you’re trying to say — other than being just a little bit off-putting? 😉
Maybe, just maybe, notwithstanding his past accomplishments, Wolfram simply has the wrong approach.
As for me, I think we will accomplish defining complexity — around about the same time as we get to a good working definition of creativity and create AI Programs.
I know, this doesn’t seem to be close at hand, but I’m hoping for a surprise.
Comment #64 September 25th, 2011 at 8:35 pm
Well, it’s not impossible because Wolfram hasn’t accomplished it. Anything
“So, you’re saying it’s impossible because Wolfram hasn’t accomplished it, because it’s “impossible” — really, your “pretty sure” about all of this?”
No. Anything’s possible, right? I think I was just giving my informal and humble views on the topic.
“What is it do think went wrong; do the the laws of physics say it’s impossible? Or, is it that humans just aren’t bright enough to “really” figure it out?”
Well, I think there exists uncomputable and irreducible things, as well as concepts that can’t be contained in a few symbols.
“And, if we haven’t, why is that, because if we had it would have been this guy Wolfram who would have manged to figured it out already?”
Although he can be a bit too ‘proud’ at times, I recognize and respect Wolfram’s genius on the topic of complexity in general.
“What is it exactly you’re trying to say — other than being just a little bit off-putting?”
Really? I was just putting forth my limited views on the matter. I guess I’m not as clever as I once thought.
“Maybe, just maybe, notwithstanding his past accomplishments, Wolfram simply has the wrong approach.”
Maybe. But as he puts it, the bits are the bits. You can’t argue with all of his results, at least.
“As for me, I think we will accomplish defining complexity — around about the same time as we get to a good working definition of creativity and create AI Programs.”
Yeah, me too. But for now, it’s between simple and random. 😉
Comment #65 September 25th, 2011 at 10:17 pm
Scott,
Have we met?… I ask as I sit absently scribbling expanded-dimensionality SR diagrams on what I’ve belatedly realize is the backside of CSAIL memo paper I picked up when I last visited the Seussaplex (yes, that’s my term, but I did get laughs with it and I don’t _think_ anyone was offended… 🙂
(Do you know Russ T? I always love hearing updates on the work he’s doing on on expanding regions of stability. It’s a mathematical approach that’s giving results intriguingly similar to biological systems, even though the underlying mechanism are entirely different, as Russ always notes. That kind of unexpected parallelism is simply intriguing!)
I thought I understood Kolmogorov complexity. Actually, I _still_ think I understand it, since I used to like to give the example of how an arbitrary string pulled deep from within pi can in principle be generated by a very short program, but good luck on figuring that out if you don’t know it’s from pi ahead of time!
The trouble is that on first whack, I just don’t get where you are heading in trying to link that particular idea with the emergence of “interesting” complexity in our universe.
If your main point is that there is likely a deep connection between seemingly mundane data compression and the workings of the physics of our universe as it stands, and that this link also ties in to how intelligent systems work, I’m absolutely with you, you’re preachin’ to the choir [SC you never read that line], etc.
In fact, I would go so far as to say that I think a deeper understanding of multilevel information factoring — data compression — needs to play a major role in the science of intelligence if we ever want to build robotic systems as small, fast, and energy-efficient as say insects.
So, I clearly need to read your ideas more closely and will try to do so soon. I’ve only skimmed, and I know it.
My blog question to you would be this: If you had to give a two-line pitch of your most critical insight or postulate to an expert — not just to some random person on an elevator! — what would it be? You could use equations, big words, small words, cryptic, or simple, just as long as it captures what you think is most important.
Maybe it’s already in there, in which case your best reply to my query may be “Go back and read paragraph x, you skxawng!” I do believe in and try to practice ego-free paper reading whenever possible… 🙂
Cheers,
Terry Bollinger
Comment #66 September 25th, 2011 at 11:17 pm
OK, since I apparently came off as unproductive to some readers, let me try to make up for it by giving my ‘more formal’ take on ‘complexodynamics”:
So it would seem that any formal definition of “complexodynamics” would necessarily require that *localized structures* can exist, that is, eventually appear and evolve and die, giving “complextropy”, within the underlying representation, say, bits here.
And it would appear that Scott’s Sophistication measure magically “picks out” these families of bit-strings that are not too simple, not too random, but just right: they have provable clusters of *localized structure*. (I say ‘magically’ here because we don’t know their origins. How were they ultimately constructed?)
So what’s going on in the coffee cups? Brownian motion. Random motion. But why should this random motion produce ‘interestingness’, or rather, temporary localized structures, at all?
Well, as time passes, the partitioned 0’s and 1’s randomly interact and trespass in each other’s initial territories. And since this interaction is indeed a random process, we *should* expect that localized structures will eventually be produced, otherwise the ‘mixing’ will occur uniformly, and hence not fit the definition of randomness, thus contradicting the brownian fluid flow under which the particles operate!
So the middle cup is ‘sophisticated’ simply because of how random processes work: flipping a fair coin does not go 0,1,0,1,…,0,1. It eventually produces temporary streaks of repetitions, or in the coffee case, temporary localized structures of ‘milk tendrils’.
But alas, as more time passes, the localized structures are forced to ultimately interact with each other, becoming highly interconnected and “smeared”, and thus disappear from effective measure.
Hence, I conclude that randomness is one origin of complexity, as it effectively takes simplicity from one end of the spectrum to the other: from partitioned, ordered elements to mixed, disordered elements.
Comment #67 September 26th, 2011 at 12:40 am
I’ll go and disagree with commenter #2 and your reply. Change plays a role of course, but it’s not the main point. If it were, you could define complexity as the time derivative of entropy, which doesn’t make much sense. Of course you can define what you want but you can come up with a lot of systems that have a steep increase in entropy without being complex in any way that we’d naively think of as complex. On that note, I also have an issue with Sean’s image of the cafe au lait, as to me it looks more like chaos than complexity.
In any case, I think Sean is right when he points out that coarse graining is important. I think the issue of change is to be found more in spatial heterogeneity. What you want is local deviations from a straight evolution towards increasing entropy, something that maintains a low entropy on the expense of entropy increase elsewhere. Again the problem is that there are systems that might have that without actually being complex, so that won’t do either, but I think that’s where one would start from.
Comment #68 September 26th, 2011 at 1:22 am
Nice work. But please don’t corrupt it with cosmological theories that might be wrong.
My favorite cosmological model, not requiring any new physics and resulting in huge conceptual simplifications, is one where the universe is infinite and matter is fractally distributed with all momenta equally represented at large enough scales. An eternal smash up because there is always a bigger and faster structure bearing down on us. Perhaps our pocket of the universe is the result of such a collision. I do believe that entropy is hard to deal with when the system is infinite. But it seems to me that if you take our local universe out to about 15 billion light years in radius and collide it with another similar or bigger pocket at 0.9999999c, the result might look like what we call the big bang. The situation would not change much even if both pockets had previously entered heat-death.
Comment #69 September 26th, 2011 at 3:17 am
Dear Scott:
You said: “First, some background: we all know the Second Law, which says that the entropy of any closed system tends to increase with time until it reaches a maximum value.”
Two points:
(i) The Second Law applies to the _thermodynamic_ _isolated_ systems, not to _all_ _closed_ systems.
Inasmuch as an information-theoretical view of entropy might perhaps differ in some manner from the real universe (i.e., from the inductive context and scope of the observations on which the Second Law was originally based), one might expect the law not to hold in an exactly similar manner in all the respects.
(ii) Off-hand, I take it that the Second Law says only that the entropy of an isolated system either remains constant or infinitesimally increases with an infinitesimal passage of time. _If_ an isolated system initially has such a level (or quantity) of entropy that it can increase with the passage of time, _then_ it will increase. The entropy’s actually reaching a maximum value, starting from a lower value, is not a part of the statement of the Second Law itself. The Second Law is equally applicable to the case wherein you have an asymptotically increasing entropy that never in fact reaches “the” (limiting) maximum value.
I have yet to read the rest of your (to me somewhat) interesting post as also all the previous comments, and so, might come back later on once again if I have any ((at least to me) interesting) comments to make. What, however, caught the eye was your inclusion of a graph which seems remarkably similar to the one which is widely studied in the chaos and nonlinear systems theory.
Best,
–Ajit
[E&OE]
Comment #70 September 26th, 2011 at 3:58 am
I would just like to comment that mkatkov (#55) and Kaleberg (#52) are pointining in directions that we know to be related.
When discussing boolean functions on the Hamming cube, the sensitivity of a function g is defined to be $\max_{x\in\left\{ 0,1\right\} ^{n}}|\{y\sim x:g(x)\neq g(y)\}|$
When the sensitivity of a function is low, we can anticipate the value of g on a point give its neighbours’ values. This is basically what mkatkov (#55) suggested.
On the other hand Kaleberg (#52) suggested that the Fourier spectrum of a function tells us something about its complexity (=interestingness). Going back to boolean functions, one can define the degree of a boolean function as a real polynomial, using its Fourier coefficients.
We know that those two notions are related (at least for boolean functions), more precisely, that $deg(g) \leq sensitivity(f)$ [Nisan & Szegedy, 94].
Comment #71 September 26th, 2011 at 5:43 am
Entropy does not increases monotonically. Even if be entropy you really mean “average entropy”, it does not increase monotonically outside the Markowian approximation.
It is not true that the Second Law says that the entropy of any closed system tends to increase with time until it reaches a maximum value. You seem to confound closed with isolated systems. Indeed, the Wikipedia article that you link uses the correct term “isolated”.
The proof that the middle picture is the more complex structure is easy, when one notices that left and rigth pictures correspond to equilibrium states. Macroscopically, complexity can be measured as deviation from equilibrium. And in very far from equilibrium regimes, appear dissipative structures, which are highly complex structures. Even a Nobel Prize was given for that. A microscopic characterization of dissipative structures is also possible.
I would add that the characterization low complexity –> high complexity –> low complexity of your example is an special case, valid when the external flows are small, there is not bifurcation points, neither memory effects. Really complex system are much more complex.
Comment #72 September 26th, 2011 at 6:57 am
Walter J Freeman III had a really good idea about complexity in his book Neurodynamics; An Exploration of Mesoscopic Brain Dynamics. [W. J. Freeman (2000)London UK: Springer-Verlag]. He observed that “self organizing” phenomena seemed to contradict the Second Law of Thermodynamics by taking on more order as time progresses. What he observed was that these phenomena were not destroying entropy, but rather they were able to organize because they were a locally cheaper way to create it. He used as an example a hurricane. This is an exaggeration of the convection rolls that are typically used as examples of self organizing phenomena. Hurricanes brew up whenever there is a sufficient amount of heat in ocean water. Without that heat and its attendant potential difference, there is no hurricane. As far as I have been able to observe, all organized systems function as accelerated entropy creation exploits.
Comment #73 September 26th, 2011 at 8:50 am
Terry Bollinger #65:
Have we met?
If we have, I don’t remember.
Do you know Russ T?
Sure.
The trouble is that on first whack, I just don’t get where you are heading in trying to link that particular idea with the emergence of “interesting” complexity in our universe.
I should have said this explicitly in this post, but the idea of linking Kolmogorov complexity with thermodynamics isn’t new at all. I didn’t invent it. In fact, in the standard textbook An Introduction to Kolmogorov Complexity and Its Applications, by Li and Vitanyi, there’s an entire chapter about this connection.
Personally, I’ve long thought that Kolmogorov complexity provides probably the most “objective,” mathematically clearest way to understand the notion of entropy—since basically, what it lets you do is talk about the “entropy” of an individual object, without reference to any hypothesized ensemble from which the object was drawn, or any hypothesized coarse-grained structure on the object. (Though actually, what you really want here is resource-bounded Kolmogorov complexity—see the several paragraphs in the post about this.) So it was completely natural for me to try to answer Sean’s question using some variation on Kolmogorov complexity as well.
My blog question to you would be this: If you had to give a two-line pitch of your most critical insight or postulate to an expert — not just to some random person on an elevator! — what would it be?
Thinking this question over, I quickly realized two things:
(1) I don’t have a “most critical insight or postulate.”
(2) It’s just as well that I don’t, since the people I can think of who do have a “most critical insight or postulate,” are the ones who I’d consider spouters and shnoods!
I mean, obviously I think things like computational complexity and quantum computing are pretty important, since otherwise I wouldn’t spend my career studying them. But I wouldn’t call the importance of these topics my “most critical insight or postulate”—since among other things, I didn’t invent them and am far from the only person who studies them!
If you’re willing to read a few hundreds or thousands of lines instead of two, you can try:
NP-complete Problems and Physical Reality
Why Philosophers Should Care About Computational Complexity
My research statement (from about 5 years ago)
Comment #74 September 26th, 2011 at 9:05 am
Peter #68:
Nice work. But please don’t corrupt it with cosmological theories that might be wrong.
As opposed to cosmological theories that are almost certainly wrong? 😉
Seriously, FWIW nothing I wrote depends on specific details of the Big Bang model—just that the universe starts in a low-entropy state and then heads toward thermal equilibrium.
Comment #75 September 26th, 2011 at 9:12 am
Juan #71:
The proof that the middle picture is the more complex structure is easy, when one notices that left and rigth pictures correspond to equilibrium states.
[Game show buzzer] Sorry, completely wrong, try again! The left picture does not correspond to an equilibrium state, and can’t possibly do so, since it evolves into the second picture.
As for the distinction between a “closed” and an “isolated” system: I don’t know what that distinction is; would anyone care to explain it? In any case, whatever the distinction is, I really don’t see how anything else in the post could have depended on it—just replace the word “closed” by the word “isolated” the one incidental place where it appears.
Comment #76 September 26th, 2011 at 10:48 am
> Why aren’t theoretical computer science conferences
> ever held on cruises? If nothing else, it certainly
> cuts down on attendees sneaking away from the
> conference venue.
I memorably attended a theoretical computer science conference (well sort of: CADE, one year) which was advertised as in a hotel on the beach at the Barrier Reef.
When you got there, you realised that this was all true, but that actually to get to the reef required an organised tour in a large boat (the conference outing of course) and the hotel was on the beach in a mining town where there was _nothing_ to do but attend the conference (or play video poker in the next room).
It is still my definition of perfect conference organisation.
Comment #77 September 26th, 2011 at 1:39 pm
Sorry, but the left picture represents an *unstable* equilibrium and any initial fluctuation will almost surely trigger the departure of the system from this initial state towards the final stable equilibrium state (the right picture). This is the reason which it evolves 🙂
The condition of equilibrium is dS=0 and the condition of stability is d^2S<0. This is similar to mechanics where both stable and unstable equilibrium states exist.
Indeed, the process that you are considering is just a mixing process. Virtually any textbook on *equilibrium* thermodynamics explain how to obtain the mixing functions (e.g. entropy of mixing, enthalpy of mixing…) from the initial and final equilibrium states.
The intermediate states of the mixing process can be studied using the tools of *nonequilibrium* thermodynamics.
Regarding your doubt, an isolated system is one in which neither energy nor mass can flow in or out. In a closed system, mass cannot flow in or out but energy can be added or removed. Contrary to what is said in this blog, the Second Law does not say that the entropy of any *closed* system tends to increase with time; the law says that (average) entropy can increase, decrease, or remain constant in function of the heat flow with the surrounds. As said above, the Wikipedia link correctly uses the term "isolated" in its discussion of the law.
As said also above, complexity can be characterized as departure from equilibrium. And in very farm from equilibrium regimes, very complex structures named dissipative arise. Microscopically this is also true. At equilibrium regimes, the dynamics is trivial and the physicochemical properties of the systems are well-described by statistical methods. Outside equilibrium that is not true. The more you depart from equilibrium, the more non-trivial is the dynamics and statistical methods lose importance.
This is the reason that works by Kolmogorov, Sinai, and others have very little impact on the physics and chemistry of nonequilibrium (The KS entropy is almost not used). Whereas works by Shanon are known to give incorrect answers to well-studied problems.
A quantitative measure of complexity is given by the degree of contraction needed to describe the system. Roughly the right picture needs a description that is about a half of the left picture, and this itself is about a half of the needed for the intermediate states.
Comment #78 September 26th, 2011 at 2:22 pm
Juan #77: No, the system on the left doesn’t represent an equilibrium at all, not even an unstable one. It’s going to start to mix even in “ideal” conditions, because of the random molecular motion of both the milk particles and the coffee particles—so it’s not at all analogous to (say) a needle balanced on its tip. This is a simple point about which you’re completely, totally, flat-out wrong.
As for the distinction you’ve drawn between “closed” and “isolated”—that the first allows transfer of energy but not mass, while the second doesn’t allow transfer of either—that seems to me like a somewhat silly distinction, one that doesn’t even make sense in a relativistic universe. It seems obvious that the sense of “closed” that’s relevant for the Second Law is that nothing should go in or out.
Comment #79 September 26th, 2011 at 4:09 pm
Scott, Sean:
I am just a layman, so much of this is above my head, however it would seem that Cosma Shalizi would be the person to ask on issues of complexity:
http://cscs.umich.edu/~crshalizi/notebooks/complexity-measures.html
Comment #80 September 26th, 2011 at 5:11 pm
Scott #73:
Ah, that helps. If your piece felt a bit open-ended to me, from your answer I gather it’s because you intended it more as a mini-intro to a topic that already has a large and fairly mature literature. I’ll read it as such.
“… you can try:
– NP-complete Problems and Physical Reality
– Why Philosophers Should Care About Computational Complexity
– My research statement (from about 5 years ago)”
Well, you may not be a shnood, but you just did an awfully good job of answering my question in a short, three-line response that is fully understandable to experts. Hmm!
(A serious question on that: Wouldn’t Maxwell and many other famous physicists qualify as big-time shnoods under that definition? A set of only four equations is pretty doggone presumptuous… what a shnood! And then there was that guy who stirred up such a ruckus with an equation that had only two variables and one constant…)
BTW, to describe myself I had to extend your list of ad hominem phrases a bit. I am clearly an extralusionary faux-intelligence. I an expert in nothing, and I apply nothing to everything, always!
As an EFI (effies always create acronyms) the question of whether or not for a given random string there exists an efficient program-like compression has always struck me — and still strikes me — as a question that is likely a lot close to the leaf nodes of physical reality that to its core. I realize you are using such ideas very differently, however, so I’ll see of any of your materials can help me see it differently.
Cheers,
Terry Bollinger
P.S. — Wolfram? Seriously? Wow.
OK: Science is all about prediction. So a serious question: What exactly did Wolfram’s massive tome (or the massive international follow-up) predict about the physical world?
I’m not aware of a single physically meaningful prediction anywhere in his book, and I went through every blasted page of it when it first came out. To the best of my knowledge, follow-up work has not changed this status.
Some terminology here:
When you specify how to predict something, AND refine that prediction by using physical evidence, it’s called science.
When you instead postulate that you have found a principle that is the key to understanding the entire universe, but you then realize you are missing the critical piece needed to make it work, so you train thousands of people about your insight and encourage them to have faith that the missing piece is out there waiting for them to help find, it’s called…
[Please, no shouts of “string theory” from the peanut gallery, I’m trying to make a real point here!… 🙂 ]
Comment #81 September 26th, 2011 at 5:50 pm
Terry Bollinger #80:
Actually, I was trying to address Sean’s new question about finding a natural complexity measure that increases and then decreases in examples like the coffee cup. As I said in the third paragraph:
My purpose, in this post, is to sketch a possible answer to Sean’s question, drawing on concepts from Kolmogorov complexity.
But in order to do that, I first had to discuss the already-known connection between Kolmogorov complexity and entropy. I’m sorry if that wasn’t clearer.
I completely disagree that Einstein and Maxwell were shnoods by my definition! As it happens, journalists did constantly ask Einstein to do things like “summarize your main idea in one sentence,” and he gave them humorous non-answers in response. That’s because he realized that translating a nontrivial idea in math or physics into “slogan” form could only lead to egregious misconceptions in someone who didn’t already know the idea. E.g., suppose he told the journalists “my main ideas are that mass is energy, and that space and time are part of the same structure,” like a salesman or politician repeating his catchphrases. People would then get an illusion of understanding that was much worse than no understanding at all. If you’re comfortable with abstract concepts, you can probably go from never having heard of special relativity to genuinely understanding something about it in only an hour, but most people aren’t interested enough to spend even that hour.
As for Wolfram, nine years ago I actually wrote the first critical academic-style review of his book, one month after it came out. In the review, I mostly focused on some incorrect claims of Wolfram’s about quantum mechanics (in the process, proving a simple corollary of Bell’s Theorem that Conway and Kochen would later call the “Free Will Theorem” 🙂 ), but there’s also some stuff in there about complexity and pseudorandomness.
Comment #82 September 26th, 2011 at 5:51 pm
I don’t think it is hard to answer Sean’s question about the three coffee cups using the notion of coarse-graining. I don’t think it is possible to define entropy without referring to the notion of coarse-graining. (I know you attempted that here, but I am not convinced about your definition. I even checked Li-Vitanyi, but they don’t seem to get rid of coarse-graining either.)
Personally, I’ve long thought that Kolmogorov complexity provides probably the most “objective,” mathematically clearest way to understand the notion of entropy—since basically, what it lets you do is talk about the “entropy” of an individual object, without reference to any hypothesized ensemble from which the object was drawn, or any hypothesized coarse-grained structure on the object.
The coarse-grained structure is not hypothesized. A crucial property of any kind of observer is that she can’t distinguish between all microstates of her surroundings. I am not very familiar with statistical mechanics, but I have a quite strong intuition that statistical mechanics is nothing but understanding all the logical implications of this single fact. Of which there are many.
Comment #83 September 26th, 2011 at 5:55 pm
Alex #79:
it would seem that Cosma Shalizi would be the person to ask on issues of complexity
I agree that Cosma is a great person to ask! But what would make anyone think that there could be one person to ask, on any subject as complex as complexity? 🙂
Comment #84 September 26th, 2011 at 6:24 pm
Hi there!
I think I came up with an easy way to measure what is intended to measure. I was trying to read all the comments to check out if someone had had the same idea, so I wouldn’t repeat it; but there are really a lot of comments and tomorrow I must wake up early… so I just hope I’m not repeating anything. If so: sorry for the bother 😉
Interesting complexity shows up when dynamics of different scales are mixed up together, so let’s take a look at the scales of the milk-coffee by Fourier transforming the milk density $M(h)$ and the coffee density $C(h)$, where $h$ is the height. We should obtain in either case the Fourier coefficients $B_w$ of the step function, where $B_w$ is the coefficient corresponding to the frequency $w$. Let’s normalize the coefficients such that $sum(B_w)=1 ==> b_w = B_w/sum(B_w)$ and reinterpret them as some weird probabilities (just imagine that we have a device which is capable of measuring one and only one spatial-frequency $w$ of the density distributions each time that it measures, and that the probability of measuring each frequency is given by $P(w)=b_w$). Then, I propose as a measure of the complexity of the system the entropy of $P(w)$.
My guess is that this quantity will obey the desired behavior. At the beginning we would have the series expansion of the step function, which has very concrete values ($P(w)$ would be a sum of Dirac’s deltas) and a relatively low entropy (low compared with what’s coming). As the milk diffuses down, the sharp distributions $P(w)$ should degenerate yielding a $P(w)$ where more $b_w$ are different from zero, so the entropy of $P(w)$ should be larger. Eventually, milk and coffee are equally distributed and the density is flat all over the cup. The Fourier transform of this thing would only have one component and the entropy would be minimal. This state will also have a lower complexity than the initial one, by the way.
This should be easy to generalize to 3D. A final remark would be that any single system should have fluctuations, thus complexity could increase and decrease several times before reaching the steady state. The law should be an averaged one, as for the usual entropy.
**Sorry for using so many times the word ‘measure’.
Comment #85 September 26th, 2011 at 7:36 pm
Scott #81:
OK, I’ve finally got the emphasis on the theme picture and the mixed-complexity domain down! It’s obvious, I know, but your emphasis helps anyway. I’ll keep an eye out for your initial framework as I read through the theory.
And yes, I was playing devil’s advocate by calling Maxwell a shnood. I knew very well that was not what you intended, but I was curious as to your response (which was quite persuasive!) If you look back at my original email, I tried to be very careful not to ask for super-simplification, but instead for some guidance on “here’s what I’m really hoping you will understand after you read through all of this.”
Interestingly, I also did a very early review of ANKoS for a software magazine. I’m wondering now if I read yours back then; your description sounds familiar. I’ll look it if I can.
Blog limit reached for the day (week?), real life calls.
Cheers,
Terry
Comment #86 September 26th, 2011 at 9:42 pm
I think it might have something to do with our universe’s rate of expansion. It’s fast(strong?) enough to pull distance galaxies away from each other, yet it’s not quite strong enough to pull particles that makes up milk and coffee apart from each other, at least not for another quintillion years. Imagine a universe with much higher rate of expansion, or one with much weaker 4 forces of nature. It wouldn’t necessarily evolve “complex” structures we observe in our universe. Having said that, the idea of “complexity” might very well be in the domain of physics, modeled as a function of other cosmic parameters, and universal peak complexity predicted.
Comment #87 September 27th, 2011 at 12:09 am
As usual, my DAH (Devil’s Advocate Hat) is on. This is convenient, because it allows you to comment on anything without doing the work to really understanding it. Thus I will proceed to disparage the notion of using Kolmogorov Complexity (KC) for anything but entertainment.
Math is a subject where a couple of interesting definitions and a few theorems can launch a subfield such as KC. I have never studied KC are tried any calculations that might give me some insight, but a brief reading of the subject suggests that it started as a joke, and today a lot of people are not in on it.
My intuition starts with the question: “How could you ever actually compute anything?”.
Furthermore, the KC of things would change as knowledge in other fields progresses. For example, what is the KC of
δ = 4.66920160910299067185320382…, and
α = 2.502907875095892822283902873218… ?
These are Feigenbaum’s constants (http://en.wikipedia.org/wiki/Feigenbaum_constants). A couple of decades ago, no one knew anything about these numbers. With the concept of analyzing discrete dynamical systems by bifurcation diagrams in hand, these can be calculated with a short program. So, did KC(δ) and KC(α) drop dramatically 20 odd years ago?
Finally, using KC reminds me of physics arguments that use the wave function for the universe. Sure, there must be such a thing, but it is hard to say much about it.
On the other side of the coin, the theorems and proofs in basic KC are rather similar to those in many fields of TCS, and many SO readers might not think of these as a joke.
BTW, V.I. Arnol’d, who made major contributions to many areas of math (and died just last year) was a student of Kolmogorov. Does anyone know if he discussed KC?
Comment #88 September 27th, 2011 at 12:40 am
(continuation) I failed to include a key point:
Given that there is a recently discovered short program for δ and α, now take any arbitrary string S, and calculate KC(S) and suppose this is a large number. Who is to say that tomorrow a new theory, perhaps arising from algorithms to gamble on FarmVille, won’t provide a short program for S, in which case KC(S) is now a small number? How could you know if this might happen?
My intuition is that the entire concept of KC is “ill-posed”, to borrow a term from PDE.
In the interest of “full disclosure”, I must mention that often in the past I have thought some topic was a bunch of hooey until I understood it, after which I thought is was profound, just like listening to Lenard Cohen.
Comment #89 September 27th, 2011 at 4:05 am
Raoul: This is indeed one of those cases where if you understood more, you’d see why your dismissal was wrong. And unlike with (say) art, music, or religion, the reasons why your dismissal is wrong can be articulated in words.
Contrary to what you say, K(x) is not undefinable: I’ll define it right now, as the length of the shortest prefix-free program (in some fixed universal programming language) that prints x and then halts! K(x) is uncomputable, but that’s a completely different issue, and something that’s been understood since the 1960s.
Basically, what K(x) lets you do is give a clear, observer-independent meaning to the loose notion of there “not existing any patterns” in a string. Already from that statement, it’s completely obvious that K(x) is going to be hard to compute—for as you correctly point out, detecting the existence or nonexistence of patterns is hard!
(Though contrary to what you say, K(Feigenbaum’s constant) didn’t suddenly become small when Feigenbaum defined the constant, any more than 42038542390523059230 suddenly became composite when I wrote it down, probably for the first time in human history! Please don’t tell me that you’re unable to distinguish between mathematical truths and our knowledge of them.)
The key point is that, even without being able to compute K(x) for most x’s, you can still use the definition of K(x) to give meaning to hundreds of intuitions that otherwise would’ve remained forever at a handwaving level. For example:
“The overwhelming majority of strings are patternless.”
“If a short computer program outputs a patternless string, then it can only be doing so by generating the string randomly.”
And many, many less obvious statements—every one of which can be upgraded to a theorem once you have a mathematical definition of “patternless.”
Furthermore, the idea of Kolmogorov complexity has actually inspired some important experimental work! For example, if you could compute K, then you could compute the “similarity” between two DNA sequences D1 and D2 by comparing
K(D1)+K(D2) to K(D1,D2).
Of course you can’t compute K, but you can compute useful upper bounds on it. For example, let G(x) be the number of bits in the gzip compression of the string x. Then comparing
G(D1)+G(D2) to G(D1,D2)
turns out to be a very useful way to measure similarity between DNA sequences.
It’s really no different from how, even though we can never tell whether a curve in the physical world is continuous or not (since that would require infinitely precise measurements), the mathematical theories dealing with continuity (e.g., calculus, topology) can still be used in physics in all sorts of ways.
Comment #90 September 27th, 2011 at 4:32 am
Dear Scott:
I have now gone through your post. Here are my (obviously) layman’s comments. (I am acutely aware of my ignorance of these topics, but, what the heck—this is just a blog-comment.)
1. First, look at the broad “structure” of the problem. With the progress of time, the entropy increases monotonically. However, in order to capture the “interesting” thing, you need to construct some other function that first increases, slows down its growth, goes through a hump, and then decreases.
Flip the graph vertically so that the hump becomes a “U”, and now it’s easier to see that this can be taken as a typical engg. optimization problem: You have to imagine _two_ factors: one that increases monotonically; another that decreases monotonically; then add the two together, and the combined function gives you the required “U” shape. For instance, the total potential energy of a mass-spring system acted upon by an applied force, or the total PE of a diatomic molecule (with attractive and repulsive forces).
(Another way to look at the hump is as the function that describes the slope of the curve in the logistic growth model, or of the S-growth curve of biology. However, the engg. optimization version brings out the necessity of having to have two oppositely acting factors more explicitly/easily.)
2. As the spring-mass model shows, you can have one of the factors increasing/decreasing linearly so long as the other factor compensates for it by decreasing/increasing more strongly than linearly, so as to ultimately produce a hump (and not a straight-line).
Thus, a linear increase of computational entropy could also be OK.
However, it seems obvious that for the physical diffusion process, the entropy should increase logarithmically. (The decreasing factor in diffusion is: the driving force (or the conc. gradient).)
3. Continuing with the hand-waving, methinks, in your idea, the algorithm that reconstructs x given the sampling oracle seems to play the part of measuring the “driving force” of the diffusion model.
4. As I said, I am quite ignorant of the actual CS theory with which this blog post of yours is mainly concerned. However, since I have already said so much, let me venture some brain-storming, with a goal of getting something concrete out of this reply.
Consider a game. Imagine a computer screen having its upper half filled with a meaningful text, and an empty bottom half. Recall those viruses that would tear away the on-screen characters/pixel-colors and drop them at random. Instead of characters, suppose the program drops down blocks of them (strings?) after chopping the text at random.
Main question: Does this game adequately bring the three coffee-cups problem into the realm of the theoretical computer science?
Secondary question: How does one deal with those words which, when chopped, produce word-fragments that still are meaningful by themselves? Or does one simply wish the problem away by simply redefining the problem to refer only to the original set of words i.e. by restricting the reference dictionary?
5. Finally, a couple of asides (about which I happen to be much more confident): (i) The objection you raised concerning the relativistic interconversion of mass and energy is irrelevant to the definitions of the closed and isolated thermodynamic systems. Closed systems are closed to the flow/exchange of matter, not of mass/energy. (ii) In the three coffee-cups problem, inasmuch as you don’t care for any other interaction of the glass-contents with the rest of the universe (and in fact exclusively focus only on the spatial rearrangements of the two constituents (including formation of tendrils, droplets, etc.)), it does qualify to be abstractly described as an isolated system—there is no exchange of anything with the surroundings to be considered here. Think about it this way: The glass-contents effectively make for the entirety of your (abstract) universe. Now, recall that the universe as a whole always forms an isolated system.
Best,
–Ajit.
[E&OE]
Comment #91 September 27th, 2011 at 10:20 am
By the left picture, I am taking an initial state at t = 0 just when the mixing starts (it seems that you also think the same when write “It’s going to start to mix”). It is rather evident that this is the case when the macroscopic flows are zero and a trivial computation gives dS = 0, which is the condition that DEFINES thermodynamic equilibrium. Indeed, any textbook writting dS >= 0 that I know emphasizes that the equality holds for equilibrium states. Evidently for 0 < t = t_rel the system is again in an equilibrium state (t_rel being the characteristic time needed to achieve equilibrium).
It seems evident to me that you are confounding equilibrium with homogeneous (an homogeneous system is an equilibrium system but the inverse is not needly true). All the processes studied in equilibrium thermodynamics textbooks belong to the kind “Initial equilibrium state” –> “Final equilibrium state” and those textbooks contains chapters devoted to the study of mixing proccesses. Those chapters explain how to obtain enthalpy of mixing, the entropy of mixing, etc. as the difference between final and initial equilibrium states. There is very little more than I can say to, except maybe to draw an entropy vs time plot for your milk-coffee system :-). Note: your diagram for the evolution of the entropy of Universe is wrong as well.
The same about the distinction between “closed” and “isolated” systems. This distinction is standard and appears in any textbook of thermodynamics or chemical thermodynamics that I know (a list can be given under request). Several online resources discuss this also (including the Wikipedia). The fact, this is the FIRST time that you hear about the existence of this distinction and of the correct form of the second law says a lot of… Your claim of that the Second Law says that “the entropy of any closed system tends to increase with time” is just plain wrong. Fortunately, the same Wikipedia article that you link does not make your notorious mistake, altough some readers could get the false impression that Wikipedia is suporting you. No it is not.
Of course, the laws of thermodynamics also work in a relativistic context. Well-informed people as Misner, Thorne, and Wheeler correctly note that the relativistic law (dS/dtau)>=0 is only valid when there is not heat flow in a system at constant composition. I.e. when the system is ISOLATED. In a closed system (dS/dtau) can be positive, negative, or zero (J_S = J_Q/T).
Your last remark is also vacuous. First because when studying the thermodynamics of the Universe we study it locally (by technical reasons that I will omit here) and saying that local entropy increases for closed systems is plain wrong. Second, because nobody has proved that Universe as a whole is an isolated system. In fact there are cosmological models where the Universe is considered an open thermodynamic system and matter born obtained from an initial unstability in a quantum spacetime without singularity involving an intermediate de Sitter regime.
Regarding the definition of complexity, your informational theory approach, even if finally satisfactory cannot provide a measure of the complexity of the dinamical laws nor of the involved time scales in the different dinamical regimes. For example, your approach to discretize the “cofee cup” to pick an adjacent coffee pixel and milk pixel uniformly at random swaping both only works if we want a description of the process for time scales much larger than a tipical memory scale t_mem and if we work with not too large gradients. Better tools are already at your hands.
Regards.
Comment #92 September 27th, 2011 at 11:19 am
There is some cool work on this kind of thing where you try to evaluate something similar to the complextropy of a string x by looking for the smallest probabilistic finite state machine that can generate x.
I suppose this boils down to roughly the same thing as the paragraph beginning “As a first step, let’s use Kolmogorov complexity to define entropy…”?
Comment #93 September 27th, 2011 at 11:30 am
Regarding Bennett’s logical depth versus (Moshe Koppel’s original notion of) sophistication: under certain formalizations of the notions, these are actually equivalent. Of course, Koppel’s notion of sophistication looks much different than Antunes and Fortnow. It’s been a while since I’ve read the Antunes/Fortnow paper, so I forget the nuances of the connection to Koppel’s work.
In particular, studying infinite sequences instead of finite strings, one can qualitatively define some sequences as deep or sophisticated, and the rest as not. There are two ways that Bennett defined depth and two ways that Koppel defined sophistication for infinite sequences. One of these ways results in depth being equivalent to sophistication. The key difference is whether we allow short programs for prefixes of an infinite sequence S to be any string, or whether we require that they themselves all are prefixes of a single infinite sequence X that is a “compressed representation” of S (despite being infinite itself).
The first notion, strong depth, is this: an infinite sequence S is strongly deep if, for all constants c, all computable time bounds t:N –> N, and all but finitely many n, every program that prints S[1..n] in time t(n) is at least c bits larger than K(S[1..n]). Surprisingly, this is shown by Bennett (and later more formally by Juedes, Lathrop and Lutz, using Levin’s Coding Theorem) to be equivalent to requiring that all t(n)-fast programs for S[1..n] are themselves compressible by at least c bits (i.e., K(p) {0,1}*, and all but finitely many n, if U(p,x) = S[1..n], then |x| > K(S[1..n]) + c.
It turns out that the strongly deep sequences coincide with the strongly sophisticated sequences.
The connection between these notions is that each defines the complexity of S in terms of the Kolmogorov complexity of prefixes of S. When considering programs that define the Kolmogorov complexity of various different prefixes of S, these programs need not have any relation to one another, even though their outputs are all prefixes of the same infinite sequence. We could instead require that the short programs we consider are prefixes of one another; i.e., we demand that there be a single infinite sequence, the prefixes of which can be used to compute prefixes of S. This leads to “weak depth” and “weak sophistication”.
A sequence is weakly deep if for all constants c, all computable time bounds t:N –> N, and all infinite sequences X, for all but finitely many n, if U^t(X[1..m]) = S[1..n], then m > K(S[1..n]) + c. This turns out to be equivalent to stating that S is not truth-table reducible to any Martin-Loef random sequence.
A sequence is weakly sophisticated if for all constants c, all total programs p, and all infinite sequences X, for all but finitely many n, if U(p,X[1..m]) = S[1..n], then m > K(S[1..n]). Again, this looks like strong sophistication as defined above, but requiring that all the candidate fast, short programs for prefixes of S themselves be prefixes of a single infinite sequence X.
Philippe Moser and I tried unsuccessfully for a while (specifically, for the length of one bus ride from Siena to Rome) to prove that weak depth is equivalent to weak sophistication, without success.
I’m not sure if any of this translates to meaningful statements about the depth or sophistication of finite strings. I know the infinite sequences versions of depth and sophistication inspired Antunes and Fortnow’s work on these concepts for finite strings, but they may have made enough changes that the concepts no longer coincide significantly.
Comment #94 September 27th, 2011 at 11:33 am
For some reason the following paragraph was chopped from my comment. Mentally insert it before “It turns out that…” in my post above:
What I will call strong sophistication is this (letting U denote a universal TM taking two input strings, p a program and an input for p): an infinite sequence S is strongly sophisticated if, for all constants c, all programs p representing a total computable function p:{0,1}* –> {0,1}*, and all but finitely many n, if U(p,x) = S[1..n], then |x| > K(S[1..n]) + c.
Comment #95 September 27th, 2011 at 11:41 am
Juan: The philosopher David Chalmers recently wrote a paper proposing that, when two people are locked in a dispute that they suspect is purely over words, what they should do is ban the problematic words from the conversation and then see whether any substantive disagreement remains. With your kind indulgence, I’d like to use this dispute as a test case for his method.
With “closed” vs. “isolated,” we don’t even have to use his method. It’s obvious that I was using the word “closed” to mean exactly the same thing you mean by “isolated,” and that indeed, the weaker property that you mean by “closed” is something that’s completely irrelevant to this discussion and that I couldn’t possibly have meant. So I’m happy to follow you and the Wikipedia entry in using “isolated.”
Regarding “equilibrium,” I have to say you’re using that word in a way that I don’t recognize from any discussion of probability or ergodic theory I’ve ever seen, but that you claim is standard. Fine. So then let’s use the term “max-entropy” for the type of equilibrium that you don’t get out of once you’re in it: i.e., the type of equilibrium that coffee is in after it’s stirred but not before, and that the universe will be in after it degenerates into radiation, but was not in at the moment of the big bang. Then anywhere I use the word “equilibrium” in the post, you can substitute “max-entropy.”
Now what are the actual, substantive disagreements that remain?
Comment #96 September 27th, 2011 at 2:35 pm
Pete:
“I suppose this boils down to roughly the same thing as the paragraph beginning “As a first step, let’s use Kolmogorov complexity to define entropy…”?”
Not really, since the work you’re referring to (Crutchfield’s epsilon-machines) is only defined for ensembles whereas Scott’s post here is about individual objects. However, Gell-Mann’s “effective complexity”, being the Kolmogorov complexity of the distribution an ensemble is drawn from, has apparently been shown to be essentially equivalent to Crutchfield’s statistical complexity measure (the entropy of the state-occupation probabilities of the epsilon-machine) by Karoline Wiesner in a talk at ECCS’11.
Karoline has also recently co-authored a paper on measures of complexity, discussing their pros and cons: http://www.maths.bris.ac.uk/~enxkw/Publications_files/Ladyman_Complex_2011.pdf . However, like Grassberger ( http://www.springerlink.com/content/l25007637531552j/ ) and many others before, the paper takes the stance that measures of complexity must be for ensembles, not individual objects, and so does not directly address the questions raised in this blog post.
Comment #97 September 27th, 2011 at 3:43 pm
A genuine confusion: how does this “complexity is highest in the middle” argument work with cyclic systems?
(Eg. a clock reaction like http://en.wikipedia.org/wiki/Belousov%E2%80%93Zhabotinsky_reaction)
Comment #98 September 28th, 2011 at 1:23 am
“And I don’t understand how one could have tachyonic neutrinos without getting CTCs as well—would anyone who accepts that possibility be kind enough to explain it to me?”
The straightforward and simple solution is a preferred frame. It is hidden as long as Lorentz symmetry is exact, but becomes observable if there are small violations of Lorentz symmetry.
There are independent arguments in favour of a preferred frame anyway, see my homepage.
Comment #99 September 28th, 2011 at 6:53 am
Peter van Emde Boas drew my attention to this blog. On monday October 2nd Amos Golan and I organize a one day conference on Philosophy of Information at the the Info-Metrics Institute in Washington DC exactly on this issue.
See: http://www.american.edu/cas/economics/info-metrics/workshop/program-2011-october.cfm
On background information regarding Kolmogorov complexity and processes.
See:
P.W. Adriaans , Between Order and Chaos: The Quest for Meaningful Information, Theory of Computing Systems, Volume 45 , Issue 4 (July 2009), Special Issue: Computation and Logic in the Real World; Guest Editors: S. Barry Cooper, Elvira Mayordomo and Andrea Sorbi Pages 650-674, 2009
and
P.Adriaans and P. Van Emdo Boas, Computation, Information, and the Arrow of Time, In COMPUTABILITY IN CONTEXT Computation and Logic in the Real World, edited by S Barry Cooper (University of Leeds, UK) & Andrea Sorbi (Universita degli Studi di Siena, Italy) (pp 1-17),
http://ebooks.worldscinet.com/ISBN/9781848162778/9781848162778_0001.html
As I am travelling I have little time to react on the contents of this blog now, but hope to find time to do this later,
Cheers Pieter Adriaans
Comment #100 September 28th, 2011 at 7:35 am
A little correction to what I said in my comment #90 above. (And isn’t there always at least one?)
The example of the spring-mass system doesn’t fit what I was trying to point out. The strain energy of the system by itself produces a bowl/well (a “U”)—i.e., even without considering the linear change to the PE of the system as effected by the applied force.
Instead, what we really needed was two different factors such that each by itself produces only a monotonically increasing/decreasing effect, i.e. not a hump/well when taken alone, even though their combined effect produces a hump/well.
In contrast, the model of a diatomic molecule does show the required behavior. (The spring-mass system does not, even if the spring is taken to be nonlinear.)
I stand corrected.
Comment #101 September 28th, 2011 at 11:46 pm
Scott is correct that when I understand more about KC I appreciate it more. (I was afraid that was going to happen!).
Decades of understanding things by working through the standard examples has not prepared me for thinking about things where you can’t calculate anything! That reminds me of my brother-in-law’s definition of an engineer: A technician who can’t fix anything.
Comment #102 September 28th, 2011 at 11:49 pm
Scott #89:
You said:
… K(x) lets you do is give a clear, observer-independent meaning to the loose notion of there “not existing any patterns” in a string… detecting the existence or nonexistence of patterns is hard! … you can still use the definition of K(x) to give meaning to hundreds of intuitions that otherwise would’ve remained forever at a handwaving level… [e.g.] “The overwhelming majority of strings are patternless.” … “If a short computer program outputs a patternless string, then it can only be doing so by generating the string randomly.”
Fascinating comments that I seriously am trying to resist for right now…
But a couple observations, what the heck, that are likely very well covered, but may be of interest to some readers anyway:
— Proximity regions: Regions “near” extreme compressions (e.g. pi subsequences), where nearness is defined by the code brevity of a transformation, are also highly compressed, if not by quite as much. E.g. pi subsequences are highly compressed, but for very long pi subsequences, the integers on quite some distance to either side are also highly compressed because they can be accessed by simple addition or subtraction functions that can be very short in comparison to a very long pi subsequences. This effect applies until the added or subtracted numbers become so long that they also become comparable in size to the pi subsequence… unless they too have their own compressions. The result becomes very complex and recursive, and “simple” statements about the absence of K. compressions becomes a lot trickier. After going through that in my head, I’m now realizing how naive my original vision of a very sparse set of flagpoles with high compression ratios was. K. compressions beget huge ranges of “nearby” compressions via further composition with shorter transforms. The resulting landscape is not just a few flagpoles, but is likely quite craggy, with the nature of the “cragginess” rather open as more short “generalization” transforms are added or explored.
— Why do K’s exist at all? If you start with very small integers and move slowly up in digit length, when and where does the concept of a K compression meaningfully begin? I would assume there is an inverse relationship with abstraction. The number 1 is extraordinarily useful because it can represent almost anything at all, provided only that the accessing entity is itself highly complex and provides huge context (“push the red button”). [This is the “V in time” model of context I talked about earlier in a CV blog entry; meaning is always provided by earlier-in-time duplications and separation of context.] Some folks tend to call that kind of versatility “abstraction,” though you could certainly describe it other ways.
–“random” just invokes external complexity, so I don’t know what that really says except that your “computer” becomes very complicated indeed. Normal computers enforce “well behaved” memory concepts that are… well, a bit boring if you compare them to the more heuristic thinks that seem to go on in biology to achieve efficient computation.
A very, very complicated computer can of course make any string it wants to (or doesn’t want to, if it allows in external sources of randomness).
Enough, I’m just idly exploring points of curiosity without having even read your references. Invariances still strike me as more critical to fundamental physics, with “interesting” complexity emerging from V splits back in time. Think e.g. how little information would mean if every electron had different physics. It is the invariance of their properties that enables higher levels of interesting complexity — all of which I assume is below the level (?) that K. theory works at?
Cheers,
Terry
P.S. Pieter Adriaans #99: Interesting seminar title and talks (quantum & new info? hmm!), but the links in the agenda did not work, at least not for me.
Comment #103 September 28th, 2011 at 11:55 pm
Pieter Adriaans #99: Correction, the links in the agenda are now working! Something corrected itself somewhere, not sure on which end.
Comment #104 September 29th, 2011 at 3:26 am
Dear Scott,
Your main idea should work.
Over the past 20-odd minutes (a time period much shorter than what it took me to type this reply down), I just manually performed the empirical version, with a 4X4 square cup, with the upper two rows black, the bottom two rows white, and a deterministic rule. At each time step, the deterministic rule pushes one black square one cell down (provided certain conditions are met, of course.) The rule does ultimately take the system “down” to a chess-board configuration (alternate B&W) as the final state. (The rule is such that it halts the process once it reaches a chess-board state—which happens to have the maximum entropy.)
There are in all 32 boundaries between _adjacent_ squares. (We drop the 8 boundaries at, say the right and the bottom edges, for symmetry: to ensure a possibility of getting infinite lattice via periodic repetition.) Define a boundary between two adjacent similar squares (BB or WW) as similar (S), and those between two adjacent dissimilar squares as dissimilar (D).
A graph of the total number of D boundary segments vs. time does empirically show an inflection. (Rapid increase, slow increase, (no increase?—this being a manual thing, I did not check all the intermediate configurations), slow increase, rapid increase.) Hence, (some normalized) “one” minus the rate of growth of number of D segments should give you a hump. (The rate of growth itself will give a bowl/well.)
Aside: The total of number of S segments follows a symmetrically opposite trend. Not surprising: D + S = 32, a constant.
Since I am a novice in TCS, I was happy with imagining how the RLE would work as the compression method.
In the initial stages, moving a black square down increases the compressed size. By destroying the “contiguous-ness” pattern, it should increase the upper bound of KC in any compression method, because most of the stuff is contiguous. In the final stages, moving a black square down increases the “alternativity” pattern, and so it should once again decrease the upper bound of KC. So, the upper bound of KC must be high somewhere in between. Can there be some fluctuations in the upper bound of KC in the intermediate stages? I am afraid this could perhaps be the case. Manual checks require real^real hard work! In any case, “as everyone knows,” the entropy only increases throughout the time.
Is the decrease in (the upper bound of) KC symmetrical around the half-time? I have no idea how to estimate this thing.
Of what use is an upper bound if we don’t know the lower bounds? No idea.
So, I am happy to leave these two questions to the TCS proper guys.
That’s about the empirical part. If something strikes me on the theoretical side, will let you know. (But you do know better than wanting to wait for my reply, don’t you?)
Just one aside before leaving. At least for this system, I have a logic whereby one could (I think) show that having a probabilistic evolution rule would not lead to an overall different outcome, though in the probabilistic case, there could be fluctuations in the middle (or more of them, if fluctuations are present also in a bounded-KC measure for the deterministic case). This should not be an issue. On the contrary, it might help make the things in the middle even more interesting to people like Sean!
I think I am done with this thread (though I will continue to read the comments here for a while). I will have a look at your paper once it is ready.
Best,
–Ajit
[E&OE]
Comment #105 September 29th, 2011 at 9:36 am
Thanks by this discussion. First, let me correct a mistake in my last post: “Evidently for 0 =0 does not hold globally and your basic assumption would be invalid.
If universe is isolated, as most experts believe, then the law holds globally. However, unless you have a new functional expression for S, you cannot compute the rate because Universe is not globally homogeneous. The standard procedure in cosmological thermodynamics is to work locally using the standard functional expression for S (See Misner, Thorne, and Wheeler). But locally, the law (dS/dtau)>=0 is only valid if you assume constant composition and not local heat flow (Misner, Thorne, and Wheeler emphasize that they are assuming *both*). Evidently composition and temperature are not constants in our Universe.
What you call “max-entropy” correspond to a stable equilibrium, defined by dS=0 (equilibrium) and d^2S<0 (stability) see #78. Evidently, the latter condition implies that S is a maximum.
Regarding your definition of complexity, it cannot differentiate situations of different complexity. Your definition only could be valid for time scales above t_mem. That is why your evolution law is so simple. When studying the fine-details of the evolution, your cell approach "subject to random nearest-neighbor mixing dynamics" is not valid. My question remains: why would I abandon a definition of complexity in term of the degree of contraction (and the characteristic time scales) by the your own?
There is much more room for our disagreement than I can write here. For instance, your attempt to study the mixing process of the “coffee cup” by discretizing it and describing the state by the number of black and white pixels (the “coffee” and “milk”) is only valid for mixing processes involving slow and small chemical gradients. Your approach is an excellent approximation for the calm mixing of the coffee and milk at your home, but it fails for studying 'violent' mixings as those what happened at very early cosmological scales.
The thermodynamic and hydrodynamic equations found in Misner, Thorne, and Wheeler are only valid for slow and small gradients in temperature, composition, pressure… The whole formalism would give wrong values for the entropy and complexity of the Universe at early times. A possibility to study fast processes and strong gradients is to use the laws of *extended thermodynamics* (see the celebrated monograph by Jou, Casas-Vázquez, and Lebon).
The main point here is that at early times complexity is larger and you need to use more complex equations (plus an extended state space) for describing processes. As a consequence, the red line in your above figure about complexity is not correct.
Regards.
Comment #106 September 29th, 2011 at 10:45 am
Hi Juan, just a quick correction: neither of the figures is mine. As I wrote in the post, both were taken directly from a talk by the physicist and cosmologist Sean Carroll, author of From Eternity to Here. So, you might need to take up your physics disagreements with him…
Comment #107 October 1st, 2011 at 1:13 pm
I have another definition for complexity.
Assume state description of a physical system converted to a string. Both Kolmogorov Complexity and Shannon Entropy would give max values in the equilibrium state in the end, same as entropy. But notice the difference, even though reproducing a particular random string require max length UTM program, a very short program can reproduce arbitrary strings which has the same SE/KC value as that random string.
So here is a new definition of complexity of a physical system at state t:
Length of the minimal UTM program that can reproduce random strings (w/ uniform probability) which has the same SE or KC value as the string of state t description.
(Assuming the UTM has access to a random number generator.)
With this definition the complexity value would me max around the middle of time frame of a system and would be minimal at the ordered start and the max entropy end.
Comment #108 October 1st, 2011 at 3:35 pm
I have to be honest and say I just simply did not have the time to read through all 106 previous comments, though many sounded interesting.
At any rate, one of the things that struck me at the conference (and which is what led to my continued harping on the entropy thing until I was shouted down by David Albet [:)]) is that we have a tendency to introduce unintentional bias even into our definitions.
Now, I like the idea of Kolmogorov complexity (a colleague of mine in the Math Dept. studies Kolmogorov entropy and I had a student a few years back who was working with me to investigate how we could use it as a generalization). But I think that we really ought to go back even further to define what these things mean.
The conference (combined with reading a bunch of E.T. Jaynes’ work) got me to start work on developing a toy universe theory in which I stripped out absolutely everything including pre-conceived notions (e.g. how can we say an empty universe is Minkowski when there’s no way to operationally verify this for such a universe since, by definition, there’s nothing in it to do the verification? And what about an empty universe with different physical laws?). In essence, I’m trying to think like Jaynes a bit – don’t take information for granted that really isn’t there.
So, in short, I think there are unintended (hidden) assumptions and biases that go into our definitions and it’s something we need to be more aware of.
Comment #109 October 1st, 2011 at 10:02 pm
One more thought. I think we tend to misunderstand entropy. First, we should be more careful than to go on “intuition,” á là Sean’s milk example above. If we did that we’d all be Aristotelians. Second, I think it is more instructive to think of entropy as a measure of the number of possible configurations of a system. In that context it makes complete sense to see the early universe as low entropy and a sputtering soup of low-energy particles in the distant future as having a high entropy. It’s just like having a box of Legos: if some of the Legos are assembled, it reduces the number of things you can build with what’s left. But if they’re all disassembled then you can build almost anything! That being said, I think the entropy of the universe at that point will have reached some kind of maximum.
Comment #110 October 4th, 2011 at 8:24 pm
On logical depth, its increase at intermediate times, and its relation to sophistication and other complexity measures.
This is primarily a comment the logical depth of finite strings and its relation to Scott’s discussion (original post and comment 9) of the coffee cup experiment. Abram Demski (comment 47) made some similar points, and Dave Doty (comment 93) nicely summarizes the theory of logical depth and sophistication for infinite strings.
“Logical depth” (http://www.research.ibm.com/people/b/bennetc/utmx.ps) formalizes the complexity of an object’s plausible causal history, as the time required for a deterministic universal computer to generate (a digitized representation of) the object from a nearly incompressible algorithmic description. Requiring the description to be incompressible or nearly so excludes descriptions that are computable from a still simpler descriptions, which would violate Occam’s razor.
In Scott’s coffee cup example, the intermediate state has a visibly complex pattern at the milk-coffee interface. This arises from a nontrivial physical process, whose simulation would require a nontrivial computation. I think the state illustrated in the middle picture is rather more complicated than could be reproduced by a discrete diffusion process of randomly swapping adjacent voxels, and likely involves convective turbulence as well as diffusion. The interface is logically deep because any near-incompressible program for generating it would need to approximate this physical evolution. The program might comprise a few bits describing the relevant dynamical laws (thermal expansion, heat conduction, fluctuations, and hydrodynamics), a few more bits describing the simple initial condition (cold milk over hot coffee), and many bits representing stochastic (thermal, chaotic, or quantum) influences on the evolution, leading to features such as the precise location of the tendrils that would occur differently if the experiment were repeated. By contrast, the final equilibrium state of the coffee is logically shallow, despite its longer temporal history, because an alternative computation could short-circuit the system’s actual evolution and generate the structure simply by calculating the thermodynamic equilibrium state under the prescribed boundary conditions. A fast-running, near-incompressible program would suffice to do so. Informally speaking, the intermediate state is deep because it contains internal evidence of a complicated causal history, while the final state is shallow because such evidence has been obliterated by the equilibration process.
Logical depth is a fundamentally dynamic measure, having units of time or machine cycles, in contrast to minimal program size (Kolmogorov
complexity) which is measured in informational units of bits. Program size enters into the definition of logical depth, but only in a secondary role, to quantify the unlikelihood that the object originated more quickly than its logical depth (an object x is defined to have logical depth d with b bits confidence iff all programs to compute it in time less than t are compressible by at least b bits). By contrast, some other proposed measures of nontrivial complexity, such as “sophistication” and “computational depth” are informational quantities like Kolmogorov complexity, but strive to measure only the nontrivial part of an object’s information content. Thus, like logical depth, they assign low complexity to random strings.
Sophistication (Koppel 88) does so by considering near-minimal-sized descriptions of x consisting of two parts, a “program” part p specifying a total function and a “data” part d giving an input to this function. The minimal size of p such that pd is a near-minimal description of x then defines the object’s sophistication, thereby formalizing the notion of the information content of the simplest computable ensemble within which x is a typical. Thus defined, sophistication is not very useful at sub-busy-beaver levels of run time, where it remains O(1) (to see this, let p be a constant program specifying a truncated version of the universal function, with run time bounded by some rapidly-growing computable function of d).
“Computational depth” (Antunes et al ’06, ’07) refers to a family of complexity measures that combine time and program size into a single quantity by taking the difference between an object’s time-penalized and plain Kolmogorov complexities. With a logarithmic penalty function—the usual choice—computational depth often corresponds roughly to subjective notions of complexity at lower levels of complexity, but underestimates the complexity of deeper objects, especially those with a small amount of deeply buried redundancy. Conversely, with an inverse busy-beaver penalty function, computational depth approximates sophistication, reflecting the equivalence between truth-table reducibility and Turing reducibility in recursively-bounded time, and is similarly insensitive to merely exponential levels of subjective complexity.
I think these infelicities of sophistication and computational depth stem from the procrustean attempt to combine time-complexity and program size into a single scalar measure. The proper role of program size is as a certifier of plausibility or significance. If considerations of program size justify a statistically significant inference about an object’s causal history, then the dynamic complexity associated with that inference can be confidently imputed to the object itself. That is the approach of logical depth.
Comment #111 October 7th, 2011 at 11:05 pm
Those interested in measures of complexity should have a look at papers of Bialek, Nemenman and Tishby:
arXiv:physics/0103076
arXiv:physics/0007070
Comment #112 October 7th, 2011 at 11:17 pm
Charles Bennett: Thanks so much for your wonderfully-informative comment, and sorry for the delay in responding!
The issue you mentioned with Koppel’s sophistication measure—that it remains O(1) if we allow arbitrary programs—is something I worried about as well. But as discussed in the post, I think this problem can be solved simply by restricting the minimization to “simple” or “efficient” programs, for almost any definition of “simple” or “efficient” one likes. And crucially, restricting attention to efficient programs is something that I’d want to do anyway, for at least two separate reasons:
1. For me, an important requirement for any “complextropy” measure is that one be able to write actual computer programs to (crudely) approximate it, in at least some cases of physical interest. So the simpler the class of programs we’re dealing with, the better.
2. While this might reflect nothing more than complexity-theoretic prejudice, I worry about the relevance to physics of any running time greater than exponential (or certainly doubly-exponential). So for example, if an n-bit string x could be generated by a log(n)-bit program that runs in 22^2^n time, but was indistinguishable from random by any o(n)-bit program running in less time, I’d be tempted to call x “incompressible for all physically-relevant purposes.”
Now, regarding the question of whether the logical depth becomes large at intermediate times in the coffee cup example. Thanks so much for explaining your intuition for why it should become large! My basic worry is the following: how do we know that there isn’t some equally-compact program that will output the intermediate states in a short (near-linear) amount of time? Such a program could conceivably work, not by simulating the whole causal history of the coffee cup, but by some more direct method that first “sketched” the milk tendrils and then filled in more details as needed. Can you give me an argument why that sort of program would require more hard-coded entropy than the sort of program you described?
Of course, you might point out that the same objection could be raised against any other “complextropy” measure! For example, how do I know that my resource-bounded sophistication measure, or Sean Carroll’s measure based on coarse-graining, will actually become large at intermediate times in the coffee-cup system? But for my and Sean’s measures, I know how to write practical computer programs that give, admittedly not the measures themselves, but certain crude approximations to them.
For Sean’s measure, what you do is to first “blur” or “smear” your bitmap, then feed the resulting image to some standard compression program (like gzip or pkzip) and measure the size of the compressed file. For the sophistication-based measure, what you do is to first compress your bitmap using some two-part code, then measure the size of the first part of the code only.
Over the past few weeks, my student Lauren Oullette has actually been coding up these crude approximations, and seeing how they behave in a simulated coffee cup. So far, we’ve found that the coarse-graining-based measure does indeed increase and then decrease as Sean sketched on his slide, though there are a few surprises that we’re still trying to understand better. I’m looking forward to seeing what happens with the sophistication-based measure.
So, let me close with the following question for you: can you give us a “crude approximation” to logical depth that we can actually calculate in practice, analogous to the “crude approximations” to coarse-grained entropy and resource-bounded sophistication that I sketched above? If so, we’ll be thrilled to code that up as well and compare it against the other two!
Comment #113 October 25th, 2011 at 5:32 am
With regard to Kolmogorov complexity and entropy, note that there’s a whole development in the theory of dynamical systems showing how to connect Kolmogorov complexity with Shannon entropy. This goes all the way back to the 60s, when Zvonkin and Levin were trying to apply Kolmogorov’s idea to various fields and see if they yield a better understanding of what was going on in those fields. Then in the 70s a formal result was proved bu Brudno. Now, I believe there’s an unrealized potential for applying Kolmogorov’s approach to system identification in quantum physics: how does the observer know what the system is that he’s going to measure, and this problem of observer identity vs system identity actually makes use of the Zvonkin-Levin connection. This is all highly speculative, of course, but I thought it was worth mentioning in this discussion about entropy and Kolmogorov complexity.
Comment #114 October 31st, 2011 at 6:15 pm
Scott,
Since you made the mistake of mentioning the faster-than-light neutrinos, this lets me mention a question that is actually closer to your line of work. You had shown if one has closed-time like curves then in that framework BQP=P=PSPACE. But, if it turned out that neutrinos were tachyons this would not in practice let one do this since it would be really difficult to send more than a tiny number of bits back using neutrinos. This leads to a question which I’m not sure how to make more precise, but essentially is: how restrictive can one be about how many bits one is allowed to send back and still be able to solve PSPACE problems in polynomial time? An obvious similar question is for problems in NP.
How natural this question is may be a function of what happens with the neutrinos. I agree that the claim is probably incorrect.
Comment #115 November 12th, 2011 at 5:06 am
“Why does “complexity” or “interestingness” of physical systems seem to increase with time and then hit a maximum and decrease, in contrast to the entropy, which of course increases monotonically?”
What an neat question!
What are some other examples of closed physical systems that evolve on this sort of “interesting roller coaster of complexity”? The milk is a self-obsessed coagulate trying to keep its surface in tact. When a bit of the surface gets messed up, other milk moves in right in behind it for a swirly, tendril dance party. It seems there’s a lot of thermodynamic potential to drive complexity in the initial conditions…like hot and cold weather fronts about to form a tornado…but with a more interesting boundary. I think the prevalence of so many complex interfaces in our Universe between environments on every scale is astounding, and that’s a source of a lot of turbulence. I’m having trouble putting to rest the thought that the pattern of the coffee in the middle of mixing tickles our brain, sort of moving through the sweet-spot of how we compress the pattern, massaging our mental models. It’s okay to think of the positions of the milk molecules requiring more bits to specify once they start swirling? Were they informed that there was a cover charge at the dance party? All because we can’t compress them with as simple of a model on our computer? They’re saying don’t worry, the caffeine hasn’t given them the nervous shakes so much to forget where they are. Aren’t they just going to dance like any other simple program that produces beautiful, complex, nested, repetitive structures before the heat gets to them and everything turns into an orgy?
Have you ever left a cup of coffee with cream on your desk for a day and a half? The patterns that the cream forms on the surface are great!
Comment #116 December 7th, 2011 at 2:47 pm
I’m a bit late with this comment, but I just noticed something. You defined K(S) as “the number of bits in the shortest computer program that outputs the elements of S and then halts”, but elsewhere (in particular, in the paper you linked from Gács, Tromp, and Vitányi), the equivalent notion is defined not in terms of a program that outputs members of S, but in terms of a program that decides S. Was that intentional, and if so, why make that distinction? Could you use the decision version to define a notion of complextropy along the same lines of what you did, and would it differ in any meaningful way?
Comment #117 December 30th, 2011 at 2:28 am
[…] to Favorites Building in part on my talk at the time conference, Scott Aaronson has a blog post about entropy and complexity that you should go read right now. It’s similar to one I’ve been contemplating myself, […]
Comment #118 December 30th, 2011 at 1:11 pm
@116:
It seems like he meant to say “decides”, since he later refers to an oracle for membership in S. Not sure.
@Scott: You mention using gzip to estimate K(), but it fails badly in a specific case:
–Take a batch of random numbers or other high-entropy file of length N
–Concatenate it with itself
–Run through gzip
The result was ~2N when I tried it, rather than ~N (give or take a constant factor) as you would expect for the Kolmogorov complexity. It seems that gzip doesn’t handle large-scale patterns in the data well, which could be relevant to complexity / complextropy research. I can guess why not (memory constraints, probably) but it still seems problematic. Does LZMA or another more sophisticated algorithm handle this better?
Comment #119 February 12th, 2012 at 8:12 pm
[…] by Sean Carroll's FQXi presentation and has been subsequently discussed by Scott Aaronson (see here and here) and Charlie […]
Comment #120 February 25th, 2012 at 5:58 pm
[…] content, as opposed to its mere randomness. A recent example is Scott Aaronson’s notion of complextropy, defined roughly as the number of bits in the smallest program for a universal computer to […]
Comment #121 March 16th, 2012 at 10:44 pm
[…] with Scott, is there any relation to his “complexodynamics” framework here? We congratulate him and Robert Wood on winning the Alan T. Waterman Award. See also this recent […]
Comment #122 June 19th, 2012 at 6:57 am
[…] complexity is desirable, but what I think you have in mind is somewhat related to this blog entry:http://www.scottaaronson.com/blo…Comment Loading… • Post • 4:57am Add […]
Comment #123 July 25th, 2012 at 4:25 pm
Scott (and Charles (Bennett)),
I think your concern about the applicability of complexity measures is legitimate. Myself and some colleagues of mine have been trying to use and evaluate information theoretic measures such as Kolmogorov Complexity and Logical Depth in real-world situations, in your words “crude approximations” of at least the “simplest versions”.
We recently published a paper (in the journal of Complexity) showing how Logical Depth can be successfully (with care) applied (the greatest challenge was the instability of timing functions in modern computers).
You may want to have a look at the paper (Image Characterization and Classification by Physical Complexity) available online at:
http://arxiv.org/abs/1006.0051
(we used the term “physical complexity” from Charles Bennett’s own suggestion in his original paper).
The results are quite interesting, first it is shown that Logical Depth (LD) does measure different properties compared to Kolmogorov Complexity (K) alone (that is LD assigns intuitively simple and random objects to the lowest complexity values, unlike K that assigns random objects the greatest complexity). Second, we also show that LD seems to classify images containing objects of different apparent complexities in a reasonable way, one in agreement with our intuition of what is complex versus random and simple.
Sincerely,
Hector Zenil
P.s. We were also tackling the question you made about the rate of complex behaviour in increasingly larger rule spaces of cellular automata, I will keep you updated if you are interested.
Comment #124 September 18th, 2012 at 11:52 am
AMS:
> You mention using gzip to estimate K(), but it fails badly in a specific case: 1. Take a batch of random numbers or other high-entropy file of length N 2. Concatenate it with itself 3. Run through gzip.
> The result was ~2N when I tried it, rather than ~N…I can guess why not (memory constraints, probably) but it still seems problematic. Does LZMA or another more sophisticated algorithm handle this better?
Yeah, I’d guess look-ahead is the main limit. But you can easily see for yourself using 7ZIP, which while not *perfect* does do a lot better than gzip apparently does. Here’s a script and output, and we’ll run it on file size from hundred kb to scores of mb range:
$ for i in {1..5000}; do echo $RANDOM; done > test.txt && cat test.txt test.txt > test2.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test.txt.7z test.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test2.txt.7z test2.txt && du -ch test.txt test.txt.7z test2.txt test2.txt.7z; rm test*.txt*
…
224K test.txt
16K test.txt.7z
448K test2.txt
16K test2.txt.7z
704K total
16K and 16K. Fantastic. Let’s get bigger:
$ for i in {1..500000}; do echo $RANDOM; done > test.txt && cat test.txt test.txt > test2.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test.txt.7z test.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test2.txt.7z test2.txt && du -ch test.txt test.txt.7z test2.txt test2.txt.7z; rm test*.txt*
…
23M test.txt
1.2M test.txt.7z
46M test2.txt
1.3M test2.txt.7z
71M total
1.2M and 1.3M. Good, but not perfect.
$ for i in {1..1000000}; do echo $RANDOM; done > test.txt && cat test.txt test.txt > test2.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test.txt.7z test.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test2.txt.7z test2.txt && du -ch test.txt test.txt.7z test2.txt test2.txt.7z; rm test*.txt*
…
47M test.txt
2.4M test.txt.7z
93M test2.txt
2.4M test2.txt.7z
144M total
Note that the 2 compressed files are very close – 2.4M and 2.4M. Great.
But we *can* blow the lookback window if we keep increasing the file size! Here is what happens if we double the file sizes yet again:
$ for i in {1..2000000}; do echo $RANDOM; done > test.txt && cat test.txt test.txt > test2.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test.txt.7z test.txt && 7z a -t7z -m0=lzma -mx=9 -mfb=64 -ms=on test2.txt.7z test2.txt && du -ch test.txt test.txt.7z test2.txt test2.txt.7z; rm test*.txt*
…
93M test.txt
4.8M test.txt.7z
186M test2.txt
9.5M test2.txt.7z
293M total
Whups! Now test.txt.7z is 4.8M and test2.txt.7z is… 9.5M. A little less than twice as large.
—————————————————————————–
Scott:
> In the interest of a full disclosure, a wonderful MIT undergrad, Lauren Oullette, recently started a research project with me where she’s trying to do exactly that. So hopefully, by the end of the semester, we’ll be able to answer Sean’s question at least at a physics level of rigor! Answering the question at a math/CS level of rigor could take a while longer.
I’ve been following the RSS feed for a long time, but I don’t recall any followup. How did the research go?
Comment #125 January 20th, 2014 at 3:57 pm
[…] an intro to entropy on Wikipedia, and also see this blog post that they referred to in their […]
Comment #126 September 29th, 2016 at 3:27 pm
[…] The First Law of Complexodynamics – Unfortunately, as we defined it above, sophistication still doesn’t do the job. For deterministic systems, the problem is the same as the one pointed out earlier for Kolmogorov complexity: we can always describe the system’s state after t time … […]
Comment #127 November 24th, 2016 at 12:47 pm
[…] in part on my talk at the time conference, Scott Aaronson has a blog post about entropy and complexity that you should go read right now. It’s similar to one I’ve been contemplating myself, […]